CF916C Jamie and Interesting Graph

Jamie has recently found undirected weighted graphs with the following properties very interesting: - The graph is connected and contains exactly $ n $ vertices and $ m $ edges. - All edge weights are integers and are in range $ [1,10^{9}] $ inclusive. - The length of shortest path from $ 1 $ to $ n $ is a prime number. - The sum of edges' weights in the minimum spanning tree (MST) of the graph is a prime number. - The graph contains no loops or multi-edges. If you are not familiar with some terms from the statement you can find definitions of them in notes section. Help Jamie construct any graph with given number of vertices and edges that is interesting!

First line of input contains 2 integers $ n $ , $ m $ 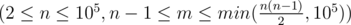 — the required number of vertices and edges.

In the first line output 2 integers $ sp $ , $ mstw $ $ (1

The graph of sample 1: 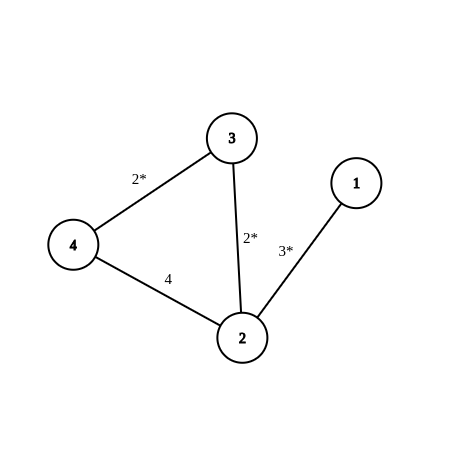 Shortest path sequence: $ {1,2,3,4} $ . MST edges are marked with an asterisk (\*). Definition of terms used in the problem statement: A shortest path in an undirected graph is a sequence of vertices $ (v_{1},v_{2},...\ ,v_{k}) $ such that $ v_{i} $ is adjacent to $ v_{i+1} $ $ 1