CF916C Jamie and Interesting Graph

Jamie 最近对具有以下性质的无向带权图产生了兴趣： - 图是连通的，且恰好包含 $n$ 个顶点和 $m$ 条边。 - 所有边的权值都是整数，并且在区间 $[1,10^{9}]$ 内。 - 从 $1$ 到 $n$ 的最短路长度是质数。 - 图的最小生成树中所有边权之和是质数。 - 图中没有自环或重边。 如果你对题目中的部分术语不熟悉，你可以在下方的“提示”部分找到它们的定义。 请你帮助 Jamie 构造一个有给定数量顶点与边，并且满足上述条件的有趣图！

输入的第一行包含两个整数 $n$ 和 $m$，即所要求的顶点和边的数量。

输出的第一行包含两个整数 $sp$ 和 $mstw$，表示最短路长度和最小生成树边权和（均满足 $1 \leq sp, mstw \leq 10^{14}$）。 接下来的 $m$ 行，每行三个整数 $u$、$v$、$w$，表示一条连接 $u$ 和 $v$ 的边，权值为 $w$。$1 \leq u, v \leq n$，$1 \leq w \leq 10^9$。

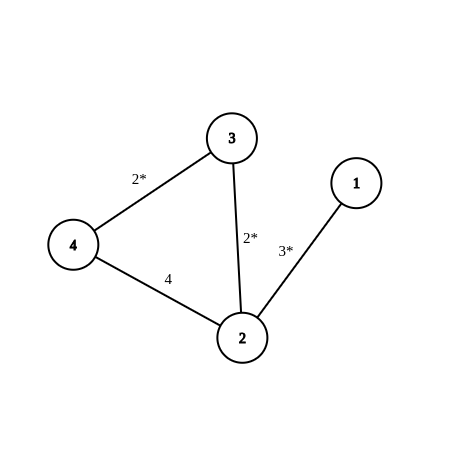
样例 1 的图如下：  最短路径为序列：$ \{1,2,3,4\} $。有 * 号标记的边属于最小生成树。 题目中提到术语的定义如下： - 无向图中的最短路指的是一条顶点序列 $ (v_{1},v_{2},... ,v_{k}) $，其中 $v_i$ 与 $v_{i+1}$ 相邻（$1 \leq i < k$），同时边权和 $ \sum w(i, j) $ （$w(i,j)$ 表示 $i$ 与 $j$ 之间的边权）达到最小。详见：[https://en.wikipedia.org/wiki/Shortest_path_problem](https://en.wikipedia.org/wiki/Shortest_path_problem) - 质数是一个大于 $1$ 且除了 $1$ 和它本身外没有其它正因数的自然数。详见：[https://en.wikipedia.org/wiki/Prime_number](https://en.wikipedia.org/wiki/Prime_number) - 最小生成树（MST）是连通无向带权图的一个边的子集，保证连通所有顶点、且无环且边权和最小。详见：[https://en.wikipedia.org/wiki/Minimum_spanning_tree](https://en.wikipedia.org/wiki/Minimum_spanning_tree) - 重边定义见：[https://en.wikipedia.org/wiki/Multiple_edges](https://en.wikipedia.org/wiki/Multiple_edges) 由 ChatGPT 5 翻译