CF916E Jamie and Tree

令你吃惊的是，Jamie 竟然是最终 BOSS！Ehehehe。 Jamie 给了你一棵有 $n$ 个结点的树，结点编号为 $1$ 到 $n$。起初，树的根为编号为 $1$ 的结点。同时，每个结点上都有一个值。 Jamie 还给了你三种类型的操作如下： $1\ v$ —— 将树的根更改为编号为 $v$ 的结点。 $2\ u\ v\ x$ —— 对于包含 $u$ 和 $v$ 的最小子树中的每个结点，将其值加上 $x$。 $3\ v$ —— 查询编号为 $v$ 的结点的子树内所有结点的值之和。 对于一个结点 $v$ 的子树，定义为所有从该结点到当前树根的最短路径经过 $v$ 的所有结点的集合。注意，改变树根后，一个结点的子树也会发生变化。 向 Jamie 展示你的编程实力，准确地完成这些操作吧！

输入的第一行包含两个用空格分隔的整数 $n$ 和 $q$（$1 \leq n \leq 10^{5}, 1 \leq q \leq 10^{5}$），分别表示树中结点数和需要处理的操作数。 第二行包含 $n$ 个用空格分隔的整数 $a_1,a_2,\ldots,a_n$（$-10^{8} \leq a_i \leq 10^{8}$），表示每个结点的初始值。 接下来的 $n-1$ 行，每行包含两个空格分隔的正整数 $u_i, v_i$（$1 \leq u_i, v_i \leq n$），描述树中的一条无向边。 接下来的 $q$ 行每行为一个操作格式，格式如下： $1\ v$（$1 \leq v \leq n$），表示第一种操作。 $2\ u\ v\ x$（$1 \leq u, v \leq n,-10^{8} \leq x \leq 10^{8}$），表示第二种操作。 $3\ v$（$1 \leq v \leq n$），表示第三种操作。 所有操作参数均为整数。 操作需按给定顺序依次执行。保证给定的结构是一棵合法的树。

对于每个第三种操作，输出一个答案。保证至少会有一个第三种操作。

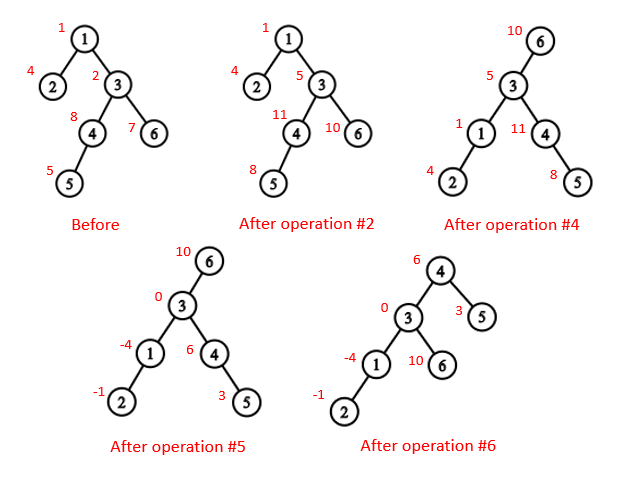
下图展示了第一个样例中，经过操作后树结构的变化。  由 ChatGPT 5 翻译