CF917B MADMAX

众所周知，Max 是她朋友中最擅长玩电子游戏的人。她的朋友们非常嫉妒她，因此专门为她设计了一个游戏，想证明她并不是最厉害的玩家。这个游戏在一张有向无环图（DAG）上进行，图有 $n$ 个顶点和 $m$ 条边。每条边上写着一个小写英文字母。  Max 和 Lucas 进行游戏。Max 先手，然后 Lucas，轮流进行。每位玩家有一个弹珠，初始时分别位于某个顶点。每到自己的回合，玩家必须沿着某条边移动自己的弹珠（若某个顶点 $v$ 有一条到 $u$ 的出边，则该玩家可以将弹珠从 $v$ 移动到 $u$）。如果玩家从顶点 $v$ 移动到顶点 $u$，那么该回合的“字符”记为从 $v$ 到 $u$ 的那条边上的字符。还有一条特殊规则：第 $i$ 回合的字符的 ASCII 码，必须大于等于第 $i-1$ 回合的字符的 ASCII 码（对于 $i>1$）。所有回合的编号，在两位玩家之间是连续编号的，也就是说 Max 是奇数编号，Lucas 是偶数编号。无法进行移动的玩家判负。两个弹珠可以同时在同一个顶点。 由于游戏可能持续很久，而 Lucas 和 Max 需要专心寻找 Dart，因此他们没有时间亲自玩，于是请你帮忙判断：若双方都以最优策略行动，谁会获胜？ 你需要输出对于所有弹珠初始位置的情况，最终的胜者。

第一行输入两个整数 $n$ 和 $m$（$2 \leq n \leq 100$，$1 \leq m \leq n(n-1)/2$）。 接下来的 $m$ 行，每行描述一条边，包含两个整数 $v$、$u$ 和一个小写英文字母 $c$，表示存在一条从 $v$ 到 $u$ 的有向边，边权为字符 $c$（$1 \leq v,u \leq n$，$v \ne u$）。任意一对顶点之间最多有一条边。保证所给图为有向无环图。

输出 $n$ 行，每行长度为 $n$ 的字符串。第 $i$ 行第 $j$ 个字符，若 Max 的弹珠起始于顶点 $i$，Lucas 的弹珠起始于顶点 $j$，且双方最优策略下，Max 获胜，则为 'A'；否则为 'B'。

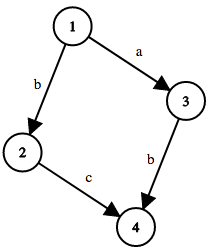
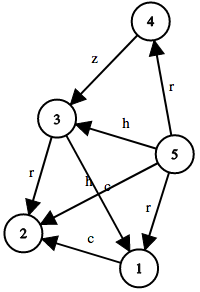
下面是第一个样例的图示：  下面是第二个样例的图示：  由 ChatGPT 5 翻译