CF919F A Game With Numbers
题目描述
假设 Alice 正在和她的朋友 Bob 玩一款纸牌游戏。他们各自手中恰好有 $8$ 张牌,每张牌上有一个整数,取值范围在 $0$ 到 $4$ 之间。在每一轮中,Alice 或 Bob 轮流从两个不同的玩家手中各选一张牌,设选中的牌上的数字分别为 $a$ 和 $b$,其中 $a$ 表示当前操作玩家的牌上的数字,$b$ 表示对手的牌上的数字。要求 $a·b≠0$。然后他们计算 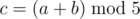,并用 $c$ 替换原来牌上的 $a$。最终,某位玩家手中的所有 $8$ 张牌上的数字均为 $0$ 时,该玩家获胜。
现在 Alice 想知道在若干种不同的局面下,谁将获胜。她会告诉你她手中每张牌的数字,Bob 手中每张牌的数字以及谁率先行动。你的任务是判断当双方都以最优策略进行游戏时,谁会获胜。
输入格式
第一行包含一个正整数 $T$($1\leq T\leq 100000$),表示需要考虑的局面数。
接下来的每组局面包含三行:
- 第一行包含一个非负整数 $f$($0\leq f\leq 1$),$f=0$ 表示 Alice 先手,$f=1$ 表示 Bob 先手。
- 第二行包含 $8$ 个非负整数 $a_{1},a_{2},...,a_{8}$($0\leq a_{i}\leq 4$),表示 Alice 的牌上的数字。
- 第三行包含 $8$ 个非负整数 $b_{1},b_{2},...,b_{8}$($0\leq b_{i}\leq 4$),表示 Bob 的牌上的数字。
保证如果 $f=0$,则 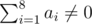。
如果 $f=1$,则 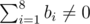。
输出格式
输出 $T$ 行。对于每种情况,判断谁会获胜。输出:
- 如果 Alice 获胜,输出 "Alice"(不带引号)。
- 如果 Bob 获胜,输出 "Bob"(不带引号)。
- 如果出现循环局面,谁也没有获胜,则输出 "Deal"(不带引号)。
说明/提示
在第一种情况下,Alice 的所有牌上数都是 $0$,因此她立即获胜。
在第二种情况下,Bob 选择 $4$ 和 $1$,因为 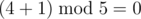,Bob 在这一步操作后赢得比赛。
在第三种情况下,Alice 选择 $1$ 和 $4$,她在这一步操作后获胜。
在第四种情况下,可以证明游戏会进入循环。
由 ChatGPT 5 翻译