CF91C Ski Base

计划在 Walrusland 建造一个滑雪基地。不过，目前项目仍处于建设阶段。建设选定了一块大型地块。地块上有 $n$ 个滑雪交叉口，编号为 $1$ 到 $n$。最初，这些交叉口之间没有任何连接。 在建设过程中，将会建造 $m$ 条双向滑雪道路。道路会依次建造：首先建造编号为 $1$ 的道路，然后是编号 $2$ 的道路，依此类推。第 $i$ 条道路连接编号为 $a_i$ 和 $b_i$ 的交叉口。 “赛道”定义为满足以下属性的路径： - 路径是封闭的，即起点和终点在同一个交叉口。 - 路径至少包含一条道路。 - 路径不会在同一条道路上重复经过，但可以经过任何一个交叉口任意多次。 我们将滑雪基地定义为已建道路的一个非空集合，该集合可以被划分为一条或多条“赛道”，并且正好每条道路属于一条赛道。此外，每条赛道只能由该集合中的道路组成。滑雪基地不要求连通。 若两个滑雪基地包含的道路集合不同，则它们被视为不同的滑雪基地。 每修建完一条新道路，Walrusland 政府都希望知道：基于当前已建道路，可以有多少种选择滑雪基地的方案。政府请你帮助他们解决这一问题。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 10^{5}, 1 \leq m \leq 10^{5}$），表示交叉口数量与道路数量。接下来 $m$ 行，每行描述一条将要修建的道路，依照建造顺序给出。每条道路用一对整数 $a_i$ 和 $b_i$ 表示（$1 \leq a_i, b_i \leq n, a_i \ne b_i$）。 同一对交叉口之间可能会有多条道路。

输出 $m$ 行，第 $i$ 行表示修建完编号为 $i$ 的道路后，能够选择滑雪基地的方案数。答案需要对 $1000000009$（$10^9+9$）取模。

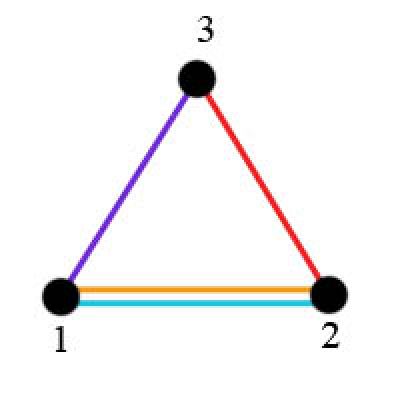
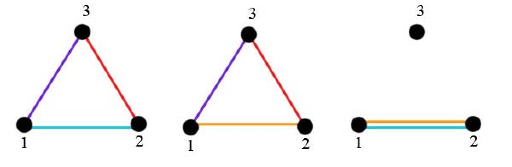
假如有 3 个交叉口，4 条道路已经全部修建好（如样例中的情况）：1 和 3，2 和 3，以及 1 和 2 之间有 2 条道路。地块的结构如下图所示：  我们可以以 3 种方式选择道路子集：  在第一种和第二种方案中，可以选择一条赛道，例如 $1$-$2$-$3$-$1$。在第一种方案中，也可以只选择 $1$-$2$-$1$ 作为一条赛道。 由 ChatGPT 5 翻译