CF924C Riverside Curio

Arkady 决定连续观察一条河流 $n$ 天。每一天河水的水位都是某个实数值。 Arkady 每天都会到河边，在河道的侧面标记当天的水位高度，但如果该高度之前已经有标记，则不会再新建标记。水不会冲刷掉这些标记。Arkady 记录下每天水面上方严格高于水位的标记数，第 $i$ 天这个值记为 $m_{i}$。 定义 $d_{i}$ 为第 $i$ 天水面下方严格低于水位的标记数。请你求出所有天数的 $d_{i}$ 之和的最小可能值。初始时河道上没有任何标记。

第一行包含一个正整数 $n$（$1 \leq n \leq 10^{5}$），表示天数。 第二行包含 $n$ 个用空格分隔的整数 $m_{1}, m_{2}, ..., m_{n}$（$0 \leq m_{i} < i$），表示每天水面上方严格高于水位的标记数。

输出一个整数，表示所有天数水面下方严格低于水位的标记数之和的最小值。

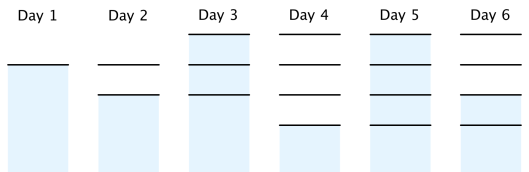
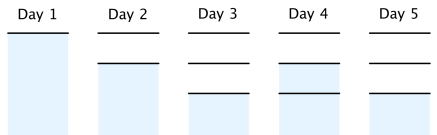
在第一个样例中，下图展示了一种最优情况。  注意在第 $3$ 天必须新建一个标记，否则第 $4$ 天无法有 $3$ 个水面上方的标记。所有天数水面下方的标记数之和为 $0+0+2+0+3+1=6$。 在第二个样例中，下图展示了一种最优情况。  由 ChatGPT 4.1 翻译