CF924E Wardrobe

Olya wants to buy a custom wardrobe. It should have $ n $ boxes with heights $ a_{1},a_{2},...,a_{n} $ , stacked one on another in some order. In other words, we can represent each box as a vertical segment of length $ a_{i} $ , and all these segments should form a single segment from $ 0 $ to 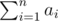 without any overlaps. Some of the boxes are important (in this case $ b_{i}=1 $ ), others are not (then $ b_{i}=0 $ ). Olya defines the convenience of the wardrobe as the number of important boxes such that their bottom edge is located between the heights $ l $ and $ r $ , inclusive. You are given information about heights of the boxes and their importance. Compute the maximum possible convenience of the wardrobe if you can reorder the boxes arbitrarily.

The first line contains three integers $ n $ , $ l $ and $ r $ ( $ 1

Print a single integer — the maximum possible convenience of the wardrobe.

In the first example you can, for example, first put an unimportant box of height $ 2 $ , then put an important boxes of sizes $ 1 $ , $ 3 $ and $ 2 $ , in this order, and then the remaining unimportant boxes. The convenience is equal to $ 2 $ , because the bottom edges of important boxes of sizes $ 3 $ and $ 2 $ fall into the range $ [3,6] $ . In the second example you have to put the short box under the tall box.