CF930D Game with Tokens
题目描述
考虑一个两人游戏。游戏中只有一个白棋子和若干个黑棋子。每个棋子都放置在平面上的一个整数坐标点 $(x, y)$ 上。
两位玩家轮流行动,由白棋先手。在每轮中,玩家可以选择将自己所有的棋子向上、下、左、右移动一个单位距离。黑棋玩家可以分别为每一个黑棋子选择移动的方向。
需要注意的是,在白棋玩家的回合结束时,白棋所在的位置不能与任何一个黑棋重合。其他棋子的摆放没有限制:黑棋可以相互重叠,黑棋回合结束时与白棋重合,以及游戏开始时白棋位于某个黑棋所在的位置都是允许的。如果白棋玩家在某一轮无法移动,则他输掉比赛。如果白棋能够成功移动 $10^{100500}$ 次,则白棋获胜。
现在的问题就是,如果黑棋子的位置已经给定,问有多少种初始位置可以放置白棋子,使得当双方都采取最佳策略时,黑棋能获胜?
输入格式
第一行包含一个整数 $n$,表示游戏中的黑棋数量($1 \le n \le 10^5$)。
接下来的 $n$ 行中,每行包含两个整数 $x_i, y_i$,表示第 $i$ 个黑棋子的初始坐标($-10^5 \le x_i, y_i \le 10^5$)。
保证所有黑棋子的初始位置互不相同。
输出格式
输出一个整数,表示白棋子开始时可以放置的初始位置数量,确保在双方都采取最佳策略的情况下,黑棋获胜。
## 提示
在第一个和第二个示例中,黑棋子的位置用黑点表示,可能的白棋初始位置(使得黑棋获胜的)用白点表示。
第一个示例: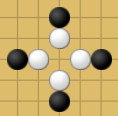
第二个示例:
在第三个示例中,白棋应该放置在内层的 $2 \times 2$ 方格中,才能确保黑棋获胜。
**本翻译由 AI 自动生成**
说明/提示
In the first and second examples initial positions of black tokens are shown with black points, possible positions of the white token (such that the black player wins) are shown with white points.
The first example: 
The second example: 
In the third example the white tokens should be located in the inner square $ 2×2 $ , to make the black player win. 