CF932D Tree

给出一个权重为 $0$ 且索引为 $1$ 的树节点。设 $cnt$ 为该树中节点的数量（初始时，$cnt$ 被设为 $1$）。支持 $Q$ 个查询，查询分为以下两种类型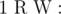： -  添加一个新节点（索引 `index` 为 $cnt + 1$）权重为 $W$，并在节点 $R$ 和此节点之间添加边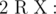； -  输出以 $R$ 为起始节点的节点序列的最大长度，该序列满足以下条件： 1. 以 $R$ 开始； 2. 序列中的每个节点都是其前驱的祖先； 3. 序列中节点的权重之和不超过 $X$； 4. 对于序列中连续的节点 $i,j$，如果 $i$ 是 $j$ 的祖先，则 $w[i] \geq w[j]$，且在从 $i$ 到 $j$ 的简单路径上不存在节点 $k$，使得 $w[k] \geq w[j]$。 树在任何时刻都以节点 $1$ 为根。 请注意，查询是以修改后的方式给出的。

第一行包含查询数量 $Q$ $(1 \leq Q \leq 400000)$。 令 $last$ 为上一个类型 $2$ 查询的答案（初始时，令 $last$ 等于 $0$）。 接下来的 $Q$ 行中，每行包含以下形式的查询： - `1 p q` ($1 \leq p, q \leq 10^{18}$)：这是第一种类型的查询，满足 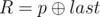 与 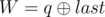。保证 $1 \leq R \leq cnt$ 且 $0 \leq W \leq 10^{9}$； - `2 p q` ($1 \leq p, q \leq 10^{18}$)：这是第二种类型的查询，满足 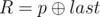 与 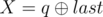。保证 $1 \leq R \leq cnt$ 且 $0 \leq X \leq 10^{15}$。  表示 $a$ 和 $b$ 的按位异或（XOR）。 保证至少存在一个类型 $2$ 的查询。

对于每个类型 $2$ 的查询，分别换行输出答案。

在样例输入 1 中，$last=0$。 \- 查询 1: `1 1 1`，节点 $2$ （权重为 $1$）被添加到节点 $1$。 \- 查询 2: `2 2 0`，以 $2$ 为起始节点的节点序列中没有权重小于等于 $0$ 的节点。此时有 $last=0$ 。 \- 查询 3: `2 2 1`，答案是 $1$，序列为 $\{2\}$。此时有 $last=1$ 。 \- 查询 4: `1 2 1`，节点 $3$ （权重为 $1$）被添加到节点 $2$。 \- 查询 5: `2 3 1`，答案是 $1$，序列为 $\{3\}$。此处节点 $2$ 不能被添加，因为权重和不能大于 $1$。此时有 $last=1$ 。 \- 查询 6: `2 3 3`，答案是 $2$，序列为 $\{3,2\}$。此时有 $last=2$ 。 > 校对：Xue Ouyang & Emma Lee from MZES.