CF933B A Determined Cleanup

In order to put away old things and welcome a fresh new year, a thorough cleaning of the house is a must. Little Tommy finds an old polynomial and cleaned it up by taking it modulo another. But now he regrets doing this... Given two integers $ p $ and $ k $ , find a polynomial $ f(x) $ with non-negative integer coefficients strictly less than $ k $ , whose remainder is $ p $ when divided by $ (x+k) $ . That is, $ f(x)=q(x)·(x+k)+p $ , where $ q(x) $ is a polynomial (not necessarily with integer coefficients).

The only line of input contains two space-separated integers $ p $ and $ k $ ( $ 1

If the polynomial does not exist, print a single integer -1, or output two lines otherwise. In the first line print a non-negative integer $ d $ — the number of coefficients in the polynomial. In the second line print $ d $ space-separated integers $ a_{0},a_{1},...,a_{d-1} $ , describing a polynomial 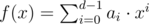 fulfilling the given requirements. Your output should satisfy $ 0

In the first example, $ f(x)=x^{6}+x^{5}+x^{4}+x=(x^{5}-x^{4}+3x^{3}-6x^{2}+12x-23)·(x+2)+46 $ . In the second example, $ f(x)=x^{2}+205x+92=(x-9)·(x+214)+2018 $ .