CF933E A Preponderant Reunion
题目描述
哪里再好,都不如自己的家好。这就是为什么过农历新年全家团聚这么重要。
在吃完团圆饭后,Tommy和他的家人们玩了一个游戏,规则如下:
1.一开始有一个由非负整数组成的序列$n$。规定无论何时数列中的每个整数都是非负的。
2.你可以在这个序列里选择两个相邻的正整数$p_i$和$p_{i+1}(1\leq i\lt n)$,然后将每个数都减去他们中的最小值$(min(p_i,p_{i+1}))$,代价为$min(p_i,p_{i+1})$。我们将此称为一次操作。
3.当数列中没有两个相邻的正整数时,游戏结束。你的任务就是用最少的代价结束游戏。
很显然,最多$n-1$次操作后游戏就会结束。请你告诉我们最优解。
输入格式
第一行是一个整数$n(1 \leq n \leq 3*10^{5})$。
第二行是$n$个整数$p_1,p_2,...,p_n(0 \leq p_i \leq 10^{9},i=1,2,...,n)$。
输出格式
第一行是一个整数$m(0 \leq m \leq n-1)$,代表操作的次数。
接下来$m$行按时间顺序输出你的操作:每行一个整数$i(1 \leq i \lt n)$代表对$p_i$和$p_{i+1}$进行如上操作。
若有多解,输出任一即可。
说明/提示
In the first sample, one possible best solution is 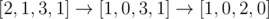, of which the cost is $ 1+1=2 $ .
In the second sample, one possible best solution is 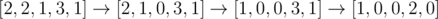, of which the cost is $ 1+1+1=3 $ .