CF935D Fafa and Ancient Alphabet

Ancient Egyptians are known to have used a large set of symbols 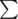 to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words $ S_{1} $ and $ S_{2} $ of equal lengths on the wall of temple written one below the other. Since this temple is very ancient, some symbols from the words were erased. The symbols in the set 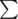 have equal probability for being in the position of any erased symbol. Fifa challenged Fafa to calculate the probability that $ S_{1} $ is lexicographically greater than $ S_{2} $ . Can you help Fafa with this task? You know that 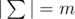, i. e. there were $ m $ distinct characters in Egyptians' alphabet, in this problem these characters are denoted by integers from $ 1 $ to $ m $ in alphabet order. A word $ x $ is lexicographically greater than a word $ y $ of the same length, if the words are same up to some position, and then the word $ x $ has a larger character, than the word $ y $ . We can prove that the probability equals to some fraction 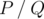, where $ P $ and $ Q $ are coprime integers, and 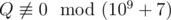. Print as the answer the value 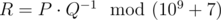, i. e. such a non-negative integer less than $ 10^{9}+7 $ , such that 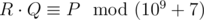, where 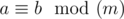 means that $ a $ and $ b $ give the same remainders when divided by $ m $ .

The first line contains two integers $ n $ and $ m $ ( $ 1

Print the value 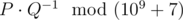, where $ P $ and $ Q $ are coprime and 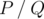 is the answer to the problem.

In the first sample, the first word can be converted into ( $ 1 $ ) or ( $ 2 $ ). The second option is the only one that will make it lexicographically larger than the second word. So, the answer to the problem will be 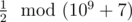, that is $ 500000004 $ , because 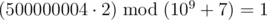. In the second example, there is no replacement for the zero in the second word that will make the first one lexicographically larger. So, the answer to the problem is 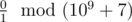, that is $ 0 $ .