CF936B Sleepy Game

Petya 和 Vasya 设计了一个游戏。游戏规则如下：玩家有一个包含 $n$ 个顶点和 $m$ 条边的有向图。其中一个顶点上有一个棋子。最开始棋子位于顶点 $s$。两位玩家轮流沿图中的某条边移动棋子。Petya 先手。无法移动棋子的一方判负。如果游戏持续 $10^{6}$ 步，则判为平局。 Vasya 因为前一天晚上在“拼写和词性”实验室做了大量实验，刚开始游戏就睡着了。Petya 决定利用这个机会，自己操作 Petya 和 Vasya 的所有回合。 你的任务是帮助 Petya 判断他是否能赢得比赛，或者至少能取得平局。

输入的第一行包含两个整数 $n$ 和 $m$，分别表示图中的顶点数和边数（$2 \leq n \leq 10^{5}$，$0 \leq m \leq 2 \cdot 10^{5}$）。 接下来的 $n$ 行描述图中的边。第 $i$ 行（$1 \leq i \leq n$）包含一个非负整数 $c_i$，表示从第 $i$ 个顶点出发的边的数量，接下来是 $c_i$ 个不同的整数 $a_{i,j}$，表示这些边指向的顶点编号（$1 \leq a_{i,j} \leq n$，$a_{i,j} \neq i$）。 保证所有 $c_i$ 的和等于 $m$。 最后一行包含一个整数 $s$，表示棋子的初始位置（$1 \leq s \leq n$）。

如果 Petya 能获胜，输出第一行 «Win»。第二行输出 $v_1, v_2, ..., v_k$（$1 \leq k \leq 10^6$），表示 Petya 获胜时应依次访问的顶点序列。$v_1$ 应等于 $s$。对于 $i=1,...,k-1$，应保证图中存在从 $v_i$ 到 $v_{i+1}$ 的边。$v_k$ 处不能再有任何可行的移动。该序列应保证 Petya 获胜。 如果 Petya 不能获胜但可以取得平局，输出一行 «Draw»。否则输出 «Lose».

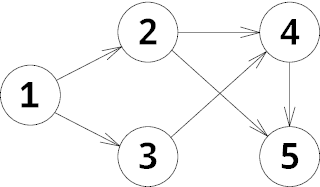
在第一个样例中，图如下所示：  最初棋子位于顶点 $1$。第一步 Petya 将棋子移动到顶点 $2$，然后为 Vasya 移动到顶点 $4$。接着 Petya 移动到顶点 $5$。此时轮到 Vasya，但已无法移动，因此 Petya 获胜。 在第二个样例中，图如下所示：  最初棋子位于顶点 $2$。Petya 唯一的选择是移动到顶点 $1$，然后为 Vasya 移动到顶点 $3$。此时轮到 Petya，但已无法移动，因此 Petya 失败。 在第三个样例中，图如下所示：  Petya 无法获胜，但可以在环上不断移动，因此双方将平局。 由 ChatGPT 4.1 翻译