CF938C Constructing Tests

Let's denote a $ m $ -free matrix as a binary (that is, consisting of only $ 1 $ 's and $ 0 $ 's) matrix such that every square submatrix of size $ m×m $ of this matrix contains at least one zero. Consider the following problem: You are given two integers $ n $ and $ m $ . You have to construct an $ m $ -free square matrix of size $ n×n $ such that the number of $ 1 $ 's in this matrix is maximum possible. Print the maximum possible number of $ 1 $ 's in such matrix. You don't have to solve this problem. Instead, you have to construct a few tests for it. You will be given $ t $ numbers $ x_{1} $ , $ x_{2} $ , ..., $ x_{t} $ . For every 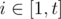, find two integers $ n_{i} $ and $ m_{i} $ ( $ n_{i}>=m_{i} $ ) such that the answer for the aforementioned problem is exactly $ x_{i} $ if we set $ n=n_{i} $ and $ m=m_{i} $ .

The first line contains one integer $ t $ ( $ 1

For each test you have to construct, output two positive numbers $ n_{i} $ and $ m_{i} $ ( $ 1