CF949F Astronomy

公元 18 年，著名天文学家 Philon the Berlander 出版了一本名为《论天空与宇宙》的书，在书中他描述了自己在夜空中观测到的不可思议的景象。他曾在晴朗的夜空中看到 $2n$ 颗星星和月亮。令人惊奇的是，可以将所有星星两两分组，使得每一对星星的连线都经过月亮的中心，并且所有这些连线都互不相同。Philon 仔细地将这种情况绘制在星空图上，并引入了坐标系。在绘制时，他注意到所有星星的中心和月亮的中心都是整数坐标点。由于 Philon 认为地球和月亮是平的，他采用了二维坐标系。天文学家选择的坐标系保证所有天体（包括月亮）的坐标绝对值都不超过 $10^{6}$。此外，没有两个天体（两颗星星或一颗星星与月亮）位于同一点。 除了星空图外，Philon 还写下了一个预言：2000 年后，星星将会处于完全相同的位置，但月亮将被一颗巨大的彗星取代，这颗彗星将毁灭地球。 现在是公元 2018 年。你得到了 Philon the Berlander 的书，并惊恐地发现，天空中的星星与 2000 年前完全相同！不幸的是，部分星空图已经遗失，现在只剩下可见星星的位置，关于星星如何分组的信息已经丢失，且图中没有月亮中心的坐标。为了找出彗星可能出现的位置并拯救人类免于毁灭，你需要立即找出一个可能的月亮中心的位置！

第一行包含一个整数 $n$（$2 \leq n \leq 2600$），表示天文学家在天空中看到的星星对数。 接下来的 $2n$ 行，每行包含两个整数 $x_i, y_i$（$-10^{6} \leq x_i, y_i \leq 10^{6}$），表示星星中心在星空图上的坐标。注意，星星的顺序是任意的，与 Philon the Berlander 所发现的星星分组无关。任意两颗星星的中心不会重合。

如果天文学家的描述不可能实现，即无法将所有点两两分组，使得所有通过这些点对的直线都是不同的、且都交于某一个整数坐标点，并且该交点不与任何星星中心重合，则输出一行 "No"（不带引号）。 否则，输出一行 "Yes"（不带引号）。第二行输出两个整数 $x, y$（$|x|, |y| \leq 10^{6}$），表示你找到的月亮中心的坐标。如果有多个答案，输出任意一个即可。注意，输出的点不能与任何星星中心重合。

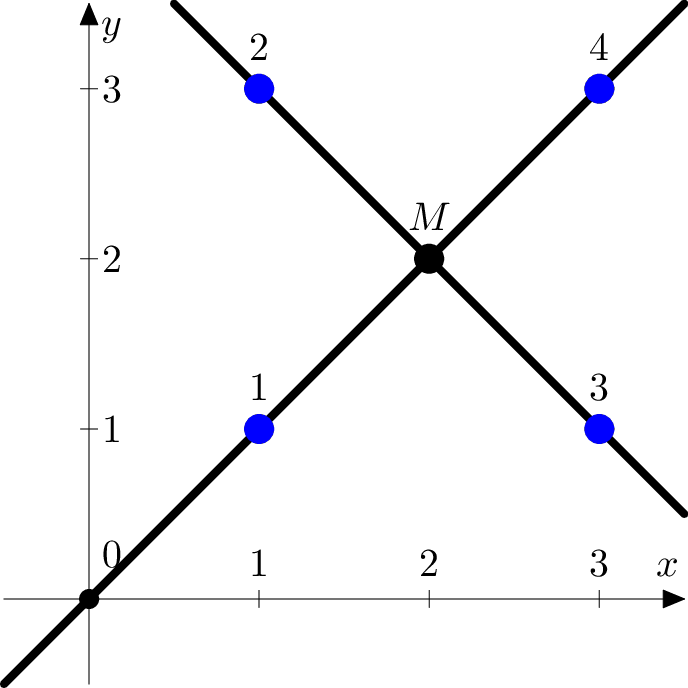
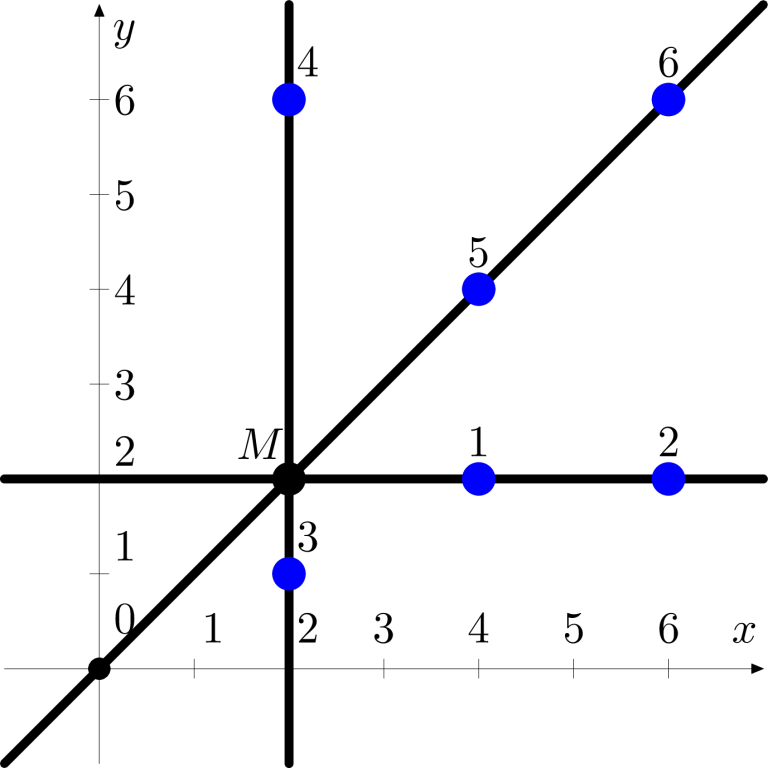
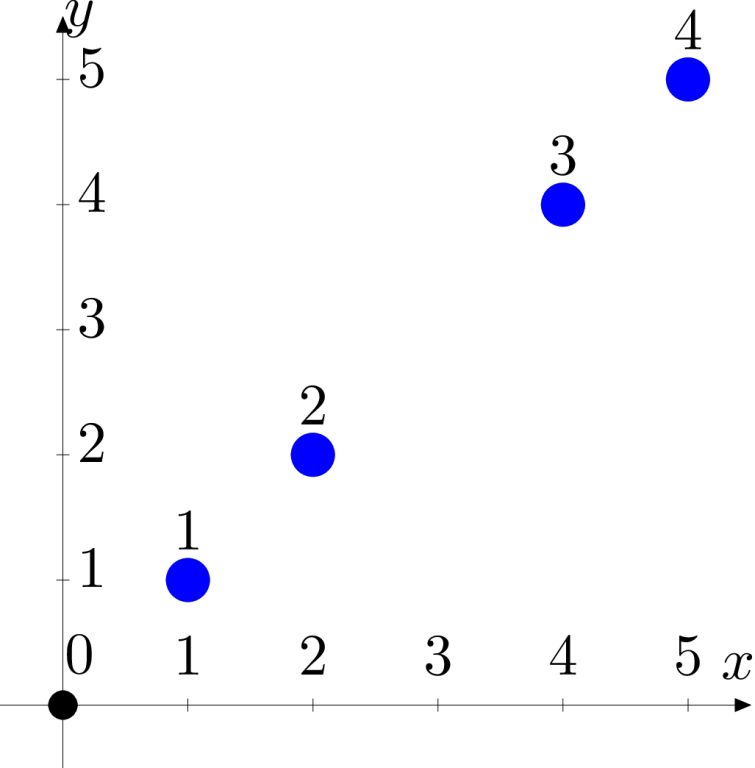
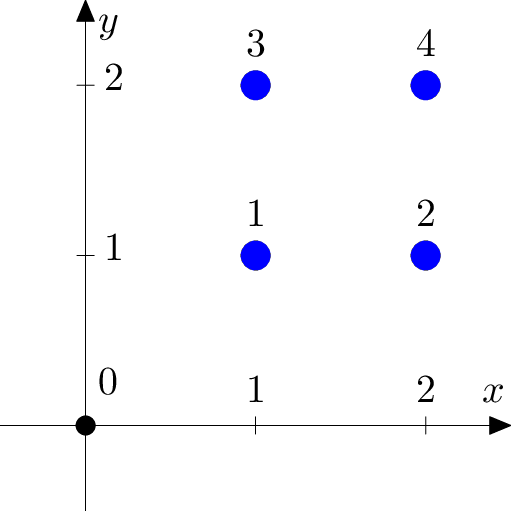
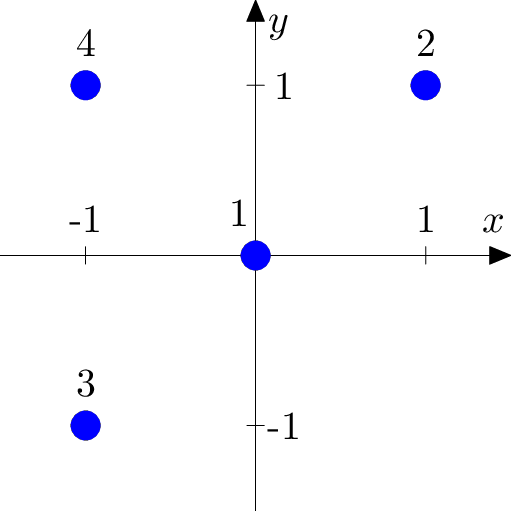
下图为样例测试的示意图。      在第四个样例测试中，月亮中心不可能在点 $(1.5, 1.5)$，因为该点坐标不是整数。 在第五个样例测试中，没有任何合适的点不与某颗星星的中心重合。 由 ChatGPT 4.1 翻译