CF954E Water Taps

Consider a system of $ n $ water taps all pouring water into the same container. The $ i $ -th water tap can be set to deliver any amount of water from $ 0 $ to $ a_{i} $ ml per second (this amount may be a real number). The water delivered by $ i $ -th tap has temperature $ t_{i} $ . If for every 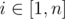 you set $ i $ -th tap to deliver exactly $ x_{i} $ ml of water per second, then the resulting temperature of water will be 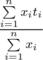 (if 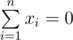, then to avoid division by zero we state that the resulting water temperature is $ 0 $ ). You have to set all the water taps in such a way that the resulting temperature is exactly $ T $ . What is the maximum amount of water you may get per second if its temperature has to be $ T $ ?

The first line contains two integers $ n $ and $ T $ ( $ 1

Print the maximum possible amount of water with temperature exactly $ T $ you can get per second (if it is impossible to obtain water with such temperature, then the answer is considered to be $ 0 $ ). Your answer is considered correct if its absolute or relative error doesn't exceed $ 10^{-6} $ .