CF954H Path Counting
题目描述
给定一棵有根树。我们用 $d(x)$ 表示节点 $x$ 的深度:根节点的深度为 $1$,其他任意节点 $x$ 的深度为其父节点 $y$ 的深度加 $1$,即 $d(x)=d(y)+1$。
这棵树具有如下性质:对于每个深度为 $i$ 的节点 $x$,它恰好有 $a_i$ 个子节点。节点的最大深度为 $n$,且 $a_n=0$。
我们定义 $f_k$ 为树中所有无序点对 $(u,v)$,使得它们之间的简单路径上边的数量恰好为 $k$ 的点对数。
请计算 $f_k \bmod 10^9+7$,对于每个 $1 \leq k \leq 2n-2$。
输入格式
输入的第一行包含一个整数 $n$($2 \leq n \leq 5000$),表示节点的最大深度。
第二行包含 $n-1$ 个整数 $a_1,a_2,\ldots,a_{n-1}$($2 \leq a_i \leq 10^9$),其中 $a_i$ 表示所有深度为 $i$ 的节点的子节点数。由于 $a_n=0$,因此输入中不包含 $a_n$。
输出格式
输出 $2n-2$ 个数,第 $k$ 个数表示 $f_k \bmod 10^9+7$。
说明/提示
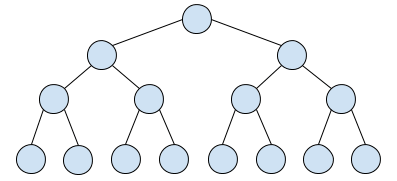
以下是第一个样例的树结构:
由 ChatGPT 4.1 翻译