CF954H Path Counting

You are given a rooted tree. Let's denote $ d(x) $ as depth of node $ x $ : depth of the root is $ 1 $ , depth of any other node $ x $ is $ d(y)+1 $ , where $ y $ is a parent of $ x $ . The tree has the following property: every node $ x $ with $ d(x)=i $ has exactly $ a_{i} $ children. Maximum possible depth of a node is $ n $ , and $ a_{n}=0 $ . We define $ f_{k} $ as the number of unordered pairs of vertices in the tree such that the number of edges on the simple path between them is equal to $ k $ . Calculate $ f_{k} $ modulo $ 10^{9}+7 $ for every $ 1

The first line of input contains an integer $ n $ ( $ 2

Print $ 2n-2 $ numbers. The $ k $ -th of these numbers must be equal to $ f_{k} $ modulo $ 10^{9}+7 $ .

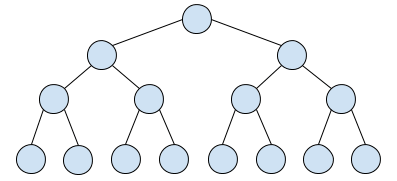
This the tree from the first sample: