CF958D2 Hyperspace Jump (hard)

现在已经是 $125$ 年过后了，但人类仍在逃离一个企图灭绝人类的机器人种族。或许我们在这里混淆了一些故事...无论如何，舰队在现在的规模更小了。然而，在最近的升级中，所有的导航系统都配备了高维线性代数跳跃处理器。 现在，为了进行迁跃，船长需要指定一个 $d$ 维空间的子空间，其中正在发生事情。她通过提供该子空间的向量生成集来实现这一点。 公主 Heidi 从 $m$ 艘船的船长那里收到了这样的一组信息。同样，她想将那些超空间迁跃子空间相等的船只分为同一组。为此，她想给每艘船分配一个 $1$ 到 $m$ 之间的组号。对于两艘船，当且仅当它们对应的子空间相等时，两艘船具有相同的组号（即使它们可能使用不同的向量集给出）。 帮帮 Heidi！ ### **简明题意** 对 $m$ 艘船每艘给出一个 $d$ 维向量集，请将目的地相同的船分在同一组。

第一行包含一个整数 $k_{i}$ $(1 \le k_i \le d)$。接下来 $k_i$ 行，第 j 行描述了第 i 艘船发送的第 j 个向量。每行包含 $d$ 个以空格分隔的整数 $a_j$ $(j = 1, ..., d)$，表示向量 $(a_1,a_2,...,a_d) \in \mathbb{R}^d$；满足 $\left\vert{a_j}\right\vert \le 250$。第 $i$ 个子空间是这 $k_i$ 个向量的线性空间。

输出 $m$ 个以空格分开的整数 $g_1,...,g_m$ $(g_i\in \{1,...,m\})$，分别表示第 $i$ 艘船的组号。对于任意的 $1 \le i < j \le m$，应满足以下条件：当且仅当第 $i$ 艘船和第 $j$ 艘船的子空间相等时，$g_i=g_j$。此外，序列 $(g_1,g_2,...,g_m)$ 应该按字典顺序在所有具有该属性的序列中最小。 ### **说明/提示** 在样例中，第一个和最后一个子空间相等，子空间 $2$ 到 $4$ 相等，子空间 $5$ 到 $7$ 相等。 思考一下，给定两个向量集 $v_1,...,v_n\in \mathbb{R}^d$ 和 $w_1,...,w_k\in\mathbb{R} ^ d$ ，如果其中一个子空间可以表示为另一个由向量组成的子空间的线性组合，那么这两个子空间是相等的。换句话说，每个向量 $v_i$ 都可以表示为向量 $w_1,...,w_k$ 的线性组合（即存在系数 $\alpha_1,...,\alpha_k$，使得 $v_i = \alpha1\omega1 + ... + \alpha k\omega k$），同样地，每个向量 $w_i$ 都可以表示为向量 $v_1,...,v_n$ 的线性组合。 再思考一下，一个序列 $(g_{1},g_{2},...,g_{m})$ 按字典顺序小于一个序列 $(h_{1},h_{2},...,h_{m})$ ，当且仅当如果存在一个序号 $i$ , $1 \le i \le m$, 使得 $g_i < h_i$ 并且对于所有 $j < i$, $g_j = h_j$。

In the sample testcase, the first and the last subspace are equal, subspaces 2 to 4 are equal, and subspaces 5 to 7 are equal. Recall that two subspaces, one given as the span of vectors 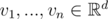 and another given as the span of vectors 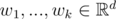, are equal if each vector $ v_{i} $ can be written as a linear combination of vectors $ w_{1},...,w_{k} $ (that is, there exist coefficients 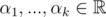 such that $ v_{i}=α_{1}w_{1}+...+α_{k}w_{k} $ ) and, similarly, each vector $ w_{i} $ can be written as a linear combination of vectors $ v_{1},...,v_{n} $ . Recall that a sequence $ (g_{1},g_{2},...,g_{m}) $ is lexicographically smaller than a sequence $ (h_{1},h_{2},...,h_{m}) $ if there exists an index $ i $ , $ 1