CF958D2 Hyperspace Jump (hard)

It is now 125 years later, but humanity is still on the run from a humanoid-cyborg race determined to destroy it. Or perhaps we are getting some stories mixed up here... In any case, the fleet is now smaller. However, in a recent upgrade, all the navigation systems have been outfitted with higher-dimensional, linear-algebraic jump processors. Now, in order to make a jump, a ship's captain needs to specify a subspace of the $ d $ -dimensional space in which the events are taking place. She does so by providing a generating set of vectors for that subspace. Princess Heidi has received such a set from the captain of each of $ m $ ships. Again, she would like to group up those ships whose hyperspace jump subspaces are equal. To do so, she wants to assign a group number between $ 1 $ and $ m $ to each of the ships, so that two ships have the same group number if and only if their corresponding subspaces are equal (even though they might be given using different sets of vectors). Help Heidi!

The first line of the input contains two space-separated integers $ m $ and $ d $ ( $ 2

Output $ m $ space-separated integers $ g_{1},...,g_{m} $ , where 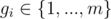 denotes the group number assigned to the $ i $ -th ship. That is, for any $ 1

In the sample testcase, the first and the last subspace are equal, subspaces 2 to 4 are equal, and subspaces 5 to 7 are equal. Recall that two subspaces, one given as the span of vectors 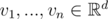 and another given as the span of vectors 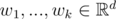, are equal if each vector $ v_{i} $ can be written as a linear combination of vectors $ w_{1},...,w_{k} $ (that is, there exist coefficients 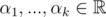 such that $ v_{i}=α_{1}w_{1}+...+α_{k}w_{k} $ ) and, similarly, each vector $ w_{i} $ can be written as a linear combination of vectors $ v_{1},...,v_{n} $ . Recall that a sequence $ (g_{1},g_{2},...,g_{m}) $ is lexicographically smaller than a sequence $ (h_{1},h_{2},...,h_{m}) $ if there exists an index $ i $ , $ 1