CF959C Mahmoud and Ehab and the wrong algorithm

Mahmoud 正在尝试解决树上的点覆盖问题。问题描述如下： 给定一棵包含 $n$ 个节点的无向树，求覆盖所有边的最小顶点数。形式化地说，我们需要找到一个顶点集合，使得对于树中的每一条边 $(u,v)$，要么 $u$ 在集合中，要么 $v$ 在集合中，或者两者都在集合中。Mahmoud 找到了如下算法： - 将树以节点 $1$ 为根。 - 统计深度为偶数的节点数，记为 $evenCnt$。 - 统计深度为奇数的节点数，记为 $oddCnt$。 - 答案为 $evenCnt$ 和 $oddCnt$ 中的较小值。 树中一个节点的深度是该节点到根节点的最短路径上的边数。根节点的深度为 $0$。 Ehab 告诉 Mahmoud 这个算法是错误的，但他不相信，因为他在许多树上测试过该算法且都正确。因此，Ehab 要求你找出两个包含 $n$ 个节点的树。对于第一棵树，该算法应输出错误答案；对于第二棵树，该算法应输出正确答案。

仅一行，包含一个整数 $n$ $(2 \leq n \leq 10^{5})$，表示所需树的节点数。

输出应包含两个独立部分，每部分对应一棵树。对于第一部分的树，算法应输出错误答案；对于第二部分的树，算法应输出正确答案。如果某部分不存在符合要求的树，则仅对该部分输出“-1”。 如果某部分存在答案，则应输出 $n-1$ 行，每行包含两个用空格分隔的整数 $u$ 和 $v$ $(1 \leq u, v \leq n)$，表示节点 $u$ 和节点 $v$ 之间有一条无向边。如果给出的图不是树或不符合格式，将判为错误答案。 如果有多种答案，可以输出任意一种。

在第一个样例中，只有一棵包含 $2$ 个节点的树（节点 $1$ 与节点 $2$ 相连）。该算法会输出正确答案，因此我们在第一部分输出 $-1$，但注意我们在第二部分输出了这棵树。 在第二个样例中： 在第一棵树中，该算法会输出 $4$ 个节点作为答案，但实际上存在只需 $3$ 个节点的方案，如下图所示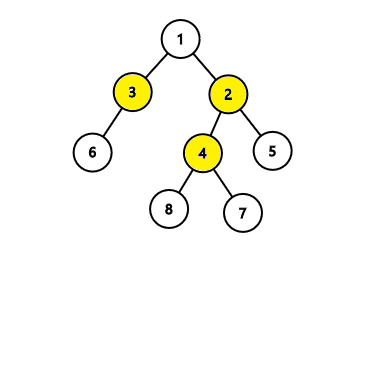： 在第二棵树中，该算法会输出 $3$ 个节点作为答案，这是正确的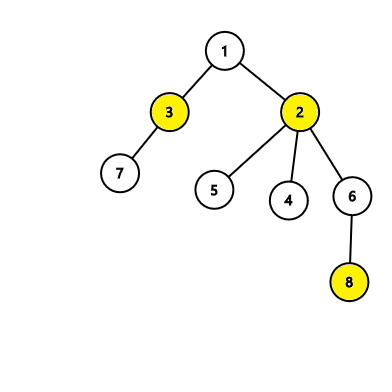： 由 ChatGPT 4.1 翻译