CF960B Minimize the error

You are given two arrays $ A $ and $ B $ , each of size $ n $ . The error, $ E $ , between these two arrays is defined 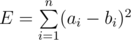. You have to perform exactly $ k_{1} $ operations on array $ A $ and exactly $ k_{2} $ operations on array $ B $ . In one operation, you have to choose one element of the array and increase or decrease it by $ 1 $ . Output the minimum possible value of error after $ k_{1} $ operations on array $ A $ and $ k_{2} $ operations on array $ B $ have been performed.

The first line contains three space-separated integers $ n $ ( $ 1

Output a single integer — the minimum possible value of 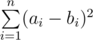 after doing exactly $ k_{1} $ operations on array $ A $ and exactly $ k_{2} $ operations on array $ B $ .

In the first sample case, we cannot perform any operations on $ A $ or $ B $ . Therefore the minimum possible error $ E=(1-2)^{2}+(2-3)^{2}=2 $ . In the second sample case, we are required to perform exactly one operation on $ A $ . In order to minimize error, we increment the first element of $ A $ by $ 1 $ . Now, $ A=[2,2] $ . The error is now $ E=(2-2)^{2}+(2-2)^{2}=0 $ . This is the minimum possible error obtainable. In the third sample case, we can increase the first element of $ A $ to $ 8 $ , using the all of the $ 5 $ moves available to us. Also, the first element of $ B $ can be reduced to $ 8 $ using the $ 6 $ of the $ 7 $ available moves. Now $ A=[8,4] $ and $ B=[8,4] $ . The error is now $ E=(8-8)^{2}+(4-4)^{2}=0 $ , but we are still left with $ 1 $ move for array $ B $ . Increasing the second element of $ B $ to $ 5 $ using the left move, we get $ B=[8,5] $ and $ E=(8-8)^{2}+(4-5)^{2}=1 $ .