CF960F Pathwalks
题目描述
给定 $n$ 个点 $m$ 条边的有向图,可能不连通,可能有重边,也可能会有自环。求最长的路径(可以经过重复节点),使得这条路径的编号和权值都**严格**单调递增,其中编号指输入的顺序。路径的长度是指经过边的数量。
输入格式
第一行两个整数 $n,m$。
第二行到第 $m+1$ 行,每行三个整数 $a,b,k$,表示顶点 $a$ 与顶点 $b$ 有一条边相连,边权为 $k$。
输出格式
一行一个整数,表示最长的路径的长度。
$1\leq n,m\leq10^5$,$0\le w_i\le10^5$。
retranslated by @皎月半洒花。
说明/提示
The answer for the first sample input is $ 2 $ : 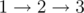. Note that you cannot traverse  because edge 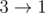 appears earlier in the input than the other two edges and hence cannot be picked/traversed after either of the other two edges.
In the second sample, it's optimal to pick $ 1 $ -st, $ 3 $ -rd and $ 5 $ -th edges to get the optimal answer: .