CF961F k-substrings

You are given a string $ s $ consisting of $ n $ lowercase Latin letters. Let's denote $ k $ -substring of $ s $ as a string $ subs_{k}=s_{k}s_{k+1}..s_{n+1-k} $ . Obviously, $ subs_{1}=s $ , and there are exactly 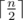 such substrings. Let's call some string $ t $ an odd proper suprefix of a string $ T $ iff the following conditions are met: - $ |T|>|t| $ ; - $ |t| $ is an odd number; - $ t $ is simultaneously a prefix and a suffix of $ T $ . For evey $ k $ -substring (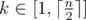) of $ s $ you have to calculate the maximum length of its odd proper suprefix.

The first line contains one integer $ n $ $ (2

Print 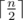 integers. $ i $ -th of them should be equal to maximum length of an odd proper suprefix of $ i $ -substring of $ s $ (or $ -1 $ , if there is no such string that is an odd proper suprefix of $ i $ -substring).

The answer for first sample test is folowing: - 1-substring: bcabcabcabcabca - 2-substring: cabcabcabcabc - 3-substring: abcabcabcab - 4-substring: bcabcabca - 5-substring: cabcabc - 6-substring: abcab - 7-substring: bca - 8-substring: c