CF961G Partitions
题目描述
给定一个包含 $n$ 个元素的集合,元素编号从 $1$ 到 $n$。第 $i$ 个元素的权值为 $w_i$。某个子集的权值记为 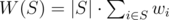。将该集合划分为 $k$ 个子集的某个划分 $R$ 的权值为 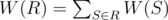(回忆一下,集合的划分是指将集合划分为若干个子集,使得每个元素恰好属于一个子集)。
请计算将给定集合划分为恰好 $k$ 个非空子集的所有划分的权值之和,并输出其对 $10^9+7$ 取模的结果。若存在两个元素 $x$ 和 $y$,在某个划分中属于同一个子集,在另一个划分中属于不同子集,则这两个划分被认为是不同的。
输入格式
第一行包含两个整数 $n$ 和 $k$($1 \leq k \leq n \leq 2 \cdot 10^5$),分别表示元素个数和每个划分中的子集个数。
第二行包含 $n$ 个整数 $w_i$($1 \leq w_i \leq 10^9$),表示集合中每个元素的权值。
输出格式
输出一个整数,表示将集合划分为 $k$ 个非空子集的所有划分的权值之和,对 $10^9+7$ 取模。
说明/提示
第一个样例的所有可能划分如下:
1. $\{\{1,2,3\},\{4\}\}$,$W(R)=3\cdot(w_1+w_2+w_3)+1\cdot w_4=24$;
2. $\{\{1,2,4\},\{3\}\}$,$W(R)=26$;
3. $\{\{1,3,4\},\{2\}\}$,$W(R)=24$;
4. $\{\{1,2\},\{3,4\}\}$,$W(R)=2\cdot(w_1+w_2)+2\cdot(w_3+w_4)=20$;
5. $\{\{1,3\},\{2,4\}\}$,$W(R)=20$;
6. $\{\{1,4\},\{2,3\}\}$,$W(R)=20$;
7. $\{\{1\},\{2,3,4\}\}$,$W(R)=26$;
第二个样例的所有可能划分如下:
1. $\{\{1,2,3,4\},\{5\}\}$,$W(R)=45$;
2. $\{\{1,2,3,5\},\{4\}\}$,$W(R)=48$;
3. $\{\{1,2,4,5\},\{3\}\}$,$W(R)=51$;
4. $\{\{1,3,4,5\},\{2\}\}$,$W(R)=54$;
5. $\{\{2,3,4,5\},\{1\}\}$,$W(R)=57$;
6. $\{\{1,2,3\},\{4,5\}\}$,$W(R)=36$;
7. $\{\{1,2,4\},\{3,5\}\}$,$W(R)=37$;
8. $\{\{1,2,5\},\{3,4\}\}$,$W(R)=38$;
9. $\{\{1,3,4\},\{2,5\}\}$,$W(R)=38$;
10. $\{\{1,3,5\},\{2,4\}\}$,$W(R)=39$;
11. $\{\{1,4,5\},\{2,3\}\}$,$W(R)=40$;
12. $\{\{2,3,4\},\{1,5\}\}$,$W(R)=39$;
13. $\{\{2,3,5\},\{1,4\}\}$,$W(R)=40$;
14. $\{\{2,4,5\},\{1,3\}\}$,$W(R)=41$;
15. $\{\{3,4,5\},\{1,2\}\}$,$W(R)=42$。
由 ChatGPT 4.1 翻译