CF962G Visible Black Areas
题目描述
Petya 有一个由 $n$ 个顶点组成的多边形。Petya 的多边形的所有边都与坐标轴平行,并且每两条相邻的边都互相垂直。保证该多边形是简单多边形,即没有自交和自接触。Petya 将多边形的所有内部区域(不包括边界)都涂成了黑色。
此外,Petya 还有一个由其坐标定义的矩形窗口,通过该窗口观察多边形。矩形窗口不能移动。矩形窗口的边也与坐标轴平行。
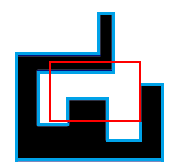 蓝色为多边形边界,红色为 Petya 的窗口。在此情况下,答案为 $2$。
请你计算,通过矩形窗口可以看到的 Petya 多边形的黑色连通区域的数量。
输入格式
第一行包含四个整数 $x_1, y_1, x_2, y_2$($x_1 < x_2$,$y_2 < y_1$),表示矩形窗口左上角和右下角的坐标。
第二行包含一个整数 $n$($4 \le n \le 15000$),表示 Petya 多边形的顶点数。
接下来的 $n$ 行,每行包含两个整数,按逆时针顺序给出 Petya 多边形的顶点坐标。保证给定的多边形满足题目描述的所有条件。
矩形窗口和多边形所有顶点的坐标均为非负整数,且不超过 $15000$。
输出格式
输出一个整数,表示通过矩形窗口可以看到的 Petya 多边形的黑色连通区域的数量。
说明/提示
样例对应上图。
由 ChatGPT 4.1 翻译