CF963C Cutting Rectangle

一个边长为 $A$ 和 $B$ 的矩形被沿其边平行的方向切割成若干个小矩形。例如，如果做了 $p$ 条水平切割和 $q$ 条垂直切割，那么切割后会剩下 $(p + 1) \times (q + 1)$ 个小矩形。切割后，这些小矩形共有 $n$ 种不同的类型。如果至少有一条边的长度不同，则认为两个矩形是不同的。注意，矩形不能旋转，也就是说，$a \times b$ 和 $b \times a$ 被认为是不同的类型（当 $a \neq b$ 时）。 对于每种类型的小矩形，给出了其边长以及这种类型的矩形的数量。 请计算有多少对 $(A, B)$ 满足可以通过切割一个边长为 $A$ 和 $B$ 的矩形得到给定的小矩形。注意，当 $A \neq B$ 时，$(A, B)$ 和 $(B, A)$ 被认为是不同的。

第一行包含一个整数 $n$（$1 \leq n \leq 2 \times 10^{5}$），表示切割后剩下的不同类型的小矩形的数量。 接下来的 $n$ 行，每行包含三个整数 $w_i, h_i, c_i$（$1 \leq w_i, h_i, c_i \leq 10^{12}$），分别表示第 $i$ 种小矩形的边长和这种类型的矩形的数量。 保证不同类型的小矩形互不相同。

输出一个整数，表示满足条件的 $(A, B)$ 对数。

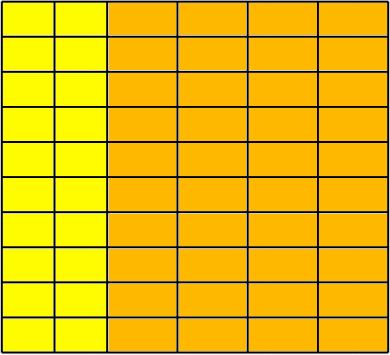
在第一个样例中，有三组满足条件的 $(A, B)$：$(1, 9)$、$(3, 3)$ 和 $(9, 1)$。 在第二个样例中，有 6 组满足条件的 $(A, B)$：$(2, 220)$、$(4, 110)$、$(8, 55)$、$(10, 44)$、$(20, 22)$ 和 $(40, 11)$。 下面是 $(20, 22)$ 的一种切割方式示意图。  第三个样例没有满足条件的对。 由 ChatGPT 4.1 翻译