CF963E Circles of Waiting

A chip was placed on a field with coordinate system onto point $ (0,0) $ . Every second the chip moves randomly. If the chip is currently at a point $ (x,y) $ , after a second it moves to the point $ (x-1,y) $ with probability $ p_{1} $ , to the point $ (x,y-1) $ with probability $ p_{2} $ , to the point $ (x+1,y) $ with probability $ p_{3} $ and to the point $ (x,y+1) $ with probability $ p_{4} $ . It's guaranteed that $ p_{1}+p_{2}+p_{3}+p_{4}=1 $ . The moves are independent. Find out the expected time after which chip will move away from origin at a distance greater than $ R $ (i.e. 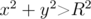 will be satisfied).

First line contains five integers $ R,a_{1},a_{2},a_{3} $ and $ a_{4} $ ( $ 0

It can be shown that answer for this problem is always a rational number of form 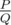, where 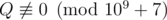. Print $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

In the first example initially the chip is located at a distance $ 0 $ from origin. In one second chip will move to distance $ 1 $ is some direction, so distance to origin will become $ 1 $ . Answers to the second and the third tests:  and 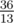.