CF975D Ghosts

幽灵们和谐共处、安宁无事，它们在空间中游荡，唯一的目的就是吓唬挡在它们路上的任何人。 宇宙中有 $n$ 个幽灵，它们在 $OXY$ 平面上移动，每个幽灵都有自己的速度，且速度不会随时间改变：$\overrightarrow{V} = V_{x}\overrightarrow{i} + V_{y}\overrightarrow{j}$，其中 $V_{x}$ 是其在 $x$ 轴上的速度，$V_{y}$ 是其在 $y$ 轴上的速度。 第 $i$ 个幽灵有一个经验值 $EX_i$，表示过去有多少个幽灵试图吓唬过它。如果两个幽灵在某一时刻出现在同一个笛卡尔坐标点上，则它们会互相吓唬。 由于幽灵们以恒定速度移动，经过一段时间后，将不会再有新的吓唬事件发生（真是松了一口气！），此时幽灵族群的经验值 $GX = \sum_{i=1}^{n} EX_i$ 将不再增加。 Tameem 是一颗红巨星，他在某一时刻 $T$ 拍摄了笛卡尔平面的一张照片，神奇的是，所有幽灵都排列在形如 $y = a \cdot x + b$ 的直线上。你的任务是计算在无限远的未来，幽灵族群的经验指数 $GX$。 注意，当 Tameem 拍照时，$GX$ 可能已经大于 $0$，因为在 $[-\infty, T]$ 的任意时刻，许多幽灵可能已经互相吓唬过了。

第一行包含三个整数 $n$、$a$ 和 $b$（$1 \leq n \leq 200000$，$1 \leq |a| \leq 10^9$，$0 \le |b| \le 10^9$）——宇宙中幽灵的数量以及直线的参数。 接下来的 $n$ 行，每行包含三个整数 $x_i$、$V_{xi}$、$V_{yi}$（$-10^9 \leq x_i \leq 10^9$，$-10^9 \leq V_{xi}, V_{yi} \leq 10^9$），其中 $x_i$ 是第 $i$ 个幽灵当前的 $x$ 坐标（且 $y_i = a \cdot x_i + b$）。 保证没有两个幽灵初始位置相同，即对于所有 $(i,j)$，$x_i \neq x_j$（$i \ne j$）。

输出一行：在无限远的未来，幽灵族群的经验指数 $GX$。

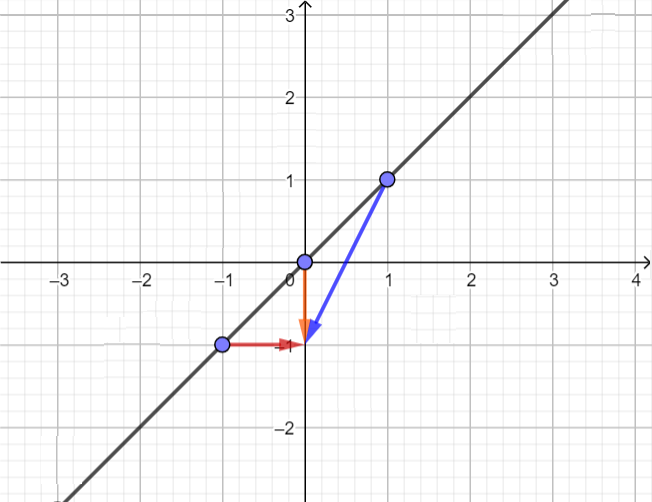
有四次碰撞，分别为 $(1,2,T-0.5)$、$(1,3,T-1)$、$(2,4,T+1)$、$(3,4,T+0.5)$，其中 $(u,v,t)$ 表示第 $u$ 个和第 $v$ 个幽灵在时刻 $t$ 发生了碰撞。每次碰撞，两个幽灵各获得一点经验值，因此 $GX = 4 \cdot 2 = 8$。 在第二个测试中，所有点将在 $t = T + 1$ 时刻发生碰撞。  红色箭头表示第 1 个幽灵的速度，橙色表示第 2 个幽灵的速度，蓝色表示第 3 个幽灵的速度。 由 ChatGPT 4.1 翻译