CF976F Minimal k-covering

You are given a bipartite graph $ G=(U,V,E) $ , $ U $ is the set of vertices of the first part, $ V $ is the set of vertices of the second part and $ E $ is the set of edges. There might be multiple edges. Let's call some subset of its edges 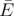 $ k $ -covering iff the graph 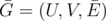 has each of its vertices incident to at least $ k $ edges. Minimal $ k $ -covering is such a $ k $ -covering that the size of the subset 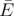 is minimal possible. Your task is to find minimal $ k $ -covering for each 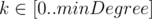, where $ minDegree $ is the minimal degree of any vertex in graph $ G $ .

The first line contains three integers $ n_{1} $ , $ n_{2} $ and $ m $ ( $ 1

For each 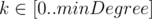 print the subset of edges (minimal $ k $ -covering) in separate line. The first integer $ cnt_{k} $ of the $ k $ -th line is the number of edges in minimal $ k $ -covering of the graph. Then $ cnt_{k} $ integers follow — original indices of the edges which belong to the minimal $ k $ -covering, these indices should be pairwise distinct. Edges are numbered $ 1 $ through $ m $ in order they are given in the input.