CF979E Kuro and Topological Parity

给定 $n$ 个点，每个点有黑白两种颜色（如果没有颜色，那么你可以把它任意涂成黑色或白色），同时你可以在这个图上任意加入一些边（当然不能加入重边或自环），要求：加入的边必须从编号小的点指向编号大的点 我们称一条好的路径为经过的点为黑白相间的路径，如果一个图好的路径的总数 $\bmod 2=p$，那么我们称这个图为好的图，现在给定你 $n$ 个点的情况，求这 $n$ 个点能组成的好的图的个数，答案对 $10^9+7$ 取模。

第一行两个整数 $n,p$，分别表示点的个数和 $p$。其中 $n\leq 50$，$p \in \{0,1\}$。 第二行 $n$ 个整数，每个整数只有三种取值：$-1,0,1$。其中，$-1$ 表示这个点未被涂色，你可以随意为他选择一种颜色，$0$ 表示这个点为黑色，$1$ 表示这个点为白色。

一行一个整数，表示答案对 $10^9+7$ 取模的结果

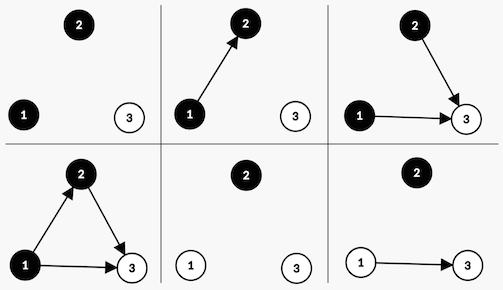
In the first example, there are $ 6 $ ways to color the pieces and add the arrows, as are shown in the figure below. The scores are $ 3, 3, 5 $ for the first row and $ 5, 3, 3 $ for the second row, both from left to right.