CF97C Winning Strategy

某所大学刚刚得知一项名为 ACM ICPC v2.0 的编程竞赛。这项竞赛与众所周知的 ACM ICPC 并无太大不同，例如，参赛选手最多只能参加两次总决赛。然而，有一个显著的不同点：每支参赛队伍必须恰好由 $n$ 名成员组成。 在多次参加 ACM ICPC v2.0 决赛且未能获得任何奖牌后，学生们和校方意识到，是时候对备赛过程进行改革了。具体来说，首项创新决定调整组队方法。经过长时间研究其他高校的赛事表现数据后，他们获得了一个有趣的信息：获奖概率与过去参加过决赛的队员人数有关。更正式地，我们已知 $n+1$ 个实数 $p_{0} \leq p_{1} \leq \ldots \leq p_{n}$，其中 $p_{i}$ 表示若本队现有 $i$ 名曾参加过决赛的成员、其余 $n-i$ 名成员首次参加决赛时，获得奖牌的概率。 尽管有了这些有用的数据，校方仍无法确定如何组队才能使 ACM ICPC v2.0 决赛获得奖牌的平均概率最大（我们假设要将这一目标长期推行，且学生们取之不尽用之不竭）。你能够提出这样的最优策略吗？在初步阶段，校方首先希望了解获得最大平均概率的具体数值。 更正式地，假设大学派出一支队伍参加第 $k$ 届世界总决赛。此队有 $a_k$ 名成员曾参加过决赛（$0 \leq a_k \leq n$）。由于每人最多只能参加两次决赛，必须满足以下条件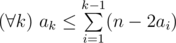：。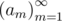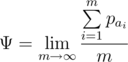你的任务是选择序列  使得下列极限 $Ψ$ 存在且数值最大：  由于 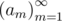 是一个无限序列，你只需输出极限 $Ψ$ 的最大值。

第一行包含一个整数 $n$（$3 \leq n \leq 100$），代表队伍成员数。 第二行包含 $n+1$ 个实数 $p_i$（$0 \leq i \leq n, 0 \leq p_i \leq 1$），表示若队中正好有 $i$ 名曾参加过决赛的成员时，该队获得奖牌的概率。并且 $p_i \leq p_{i+1}$ 对于所有 $0 \leq i \leq n-1$ 都成立，这些实数的小数点后不超过 6 位。

输出一个实数，表示如果采用最优策略，每年平均获得奖牌数量的期望值。结果的绝对或相对误差需不超过 $10^{-6}$。

在第二个测试点，无论队伍组成如何，获奖都已成定局。 由 ChatGPT 5 翻译