CF982E Billiard
题目描述
考虑一个尺寸为 $n \times m$ 的矩形台球桌,带有四个球袋。我们引入一个坐标系,原点位于左下角(见下图)。
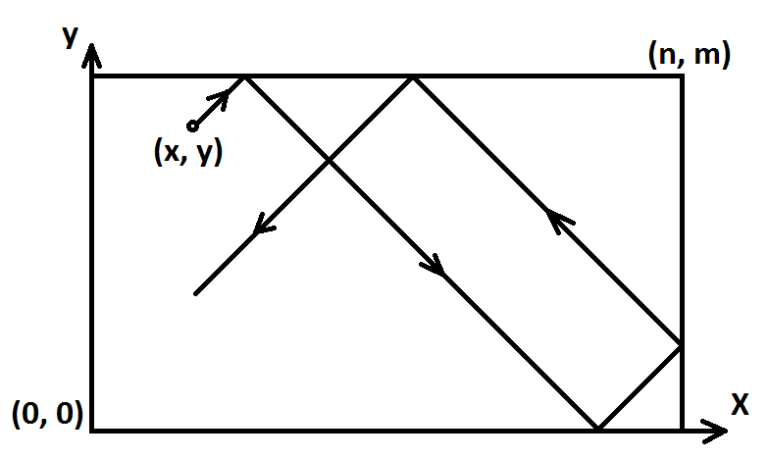
当前有一个球位于点 $(x, y)$。Max 走到球桌旁击打了球。球开始沿着与坐标轴平行或与坐标轴成 $45^\circ$ 角的直线运动。我们假设:
1. 球与边界碰撞前后的运动方向夹角相等;
2. 球会无限运动,只有当它落入球袋时才会停止;
3. 球可以视为一个点,只有当其坐标与某个球袋完全重合时才会落袋;
4. 初始时球不在任何一个球袋中。
注意,球可以沿着某条边运动,这种情况下球会直接落入该边末端的球袋。
你的任务是判断球最终是否会落入某个球袋,如果会,请输出它会落入哪一个球袋。
输入格式
一行包含 $6$ 个整数 $n$、$m$、$x$、$y$、$v_x$、$v_y$($1 \leq n, m \leq 10^9$,$0 \leq x \leq n$,$0 \leq y \leq m$,$-1 \leq v_x, v_y \leq 1$,$(v_x, v_y) \neq (0, 0)$)——分别表示球桌的宽度、长度、球的初始 $x$ 坐标、球的初始 $y$ 坐标、球初始速度的 $x$ 分量和 $y$ 分量。保证球初始时不在球袋中。
输出格式
输出球最终会落入的球袋的坐标,如果球会无限运动而不会落袋,则输出 $-1$。
说明/提示
第一个样例:
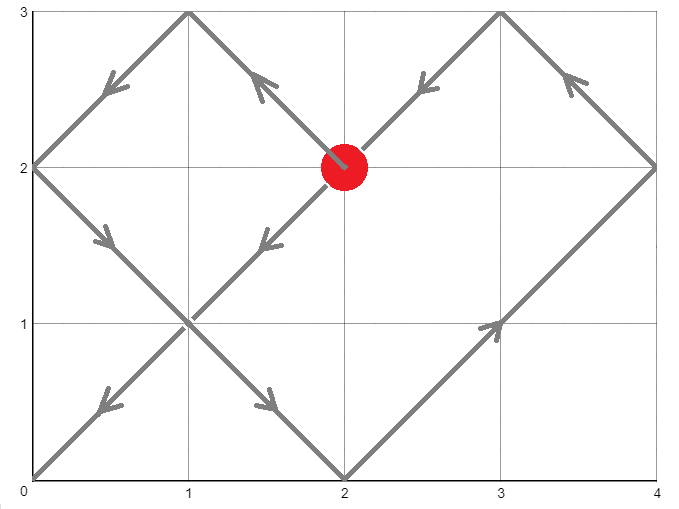
第二个样例:
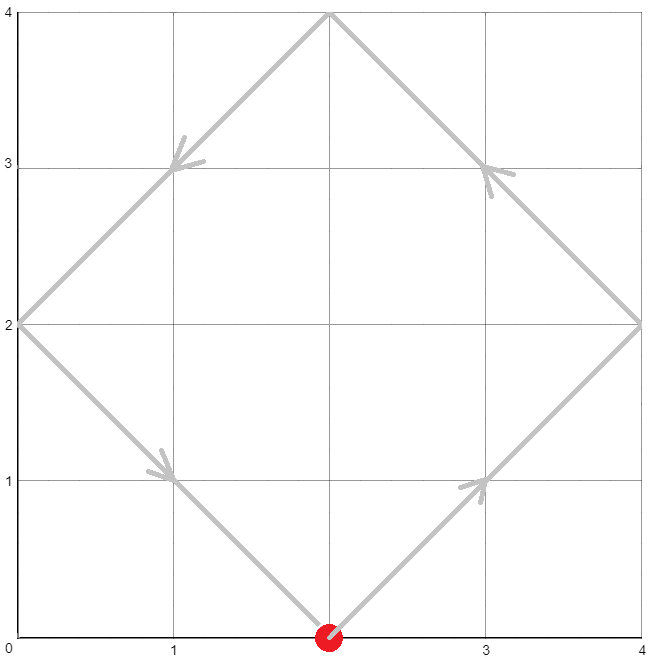
在第三个样例中,球的 $y$ 坐标永远不会改变,因此球永远不会落入球袋。
由 ChatGPT 4.1 翻译