CF983C Elevator

## 题意 一个 $9$ 层的楼有一个可以容纳 $4$ 个人的电梯，你要管理这个电梯。 现在各层楼上有一些在排队的人，你知道他们在哪层要到哪层去。你也知道到电梯门口的顺序。根据公司的规定，如果一个人比其他人早到。他也必须先进电梯（无论楼层，只凭时间）。注意人们可以随时离开电梯。 电梯有两个命令： * 上楼或者下楼， 代价为 $1$。 * 打开当前楼层的门，所有到目的地的人会从电梯里出来，当前楼层排队的人会在**不违反规定的情况下**一个一个进（在电梯还有空间的情况下），每个人用 $1$ 秒时间来出入电梯。 最初电梯是空的，在 $1$ 楼。你需要求出最少用多长时间来把所有人送回到目的地。最后电梯可以停在任意位置。

* 第一行一个整数 ： 人数 $N$ （$1 \le N \le 2000$） * 之后 $n$ 行：第 $i$ 行包含两个整数 $A_i,B_i$ （$1 \le A_i,B_i \le 9, A_i \ne B_i$）-- $A_i$ 表示最初楼层，$B_i$ 表示目的楼层。到达电梯门口的顺序按输入顺序排序。

* 一个整数，表示以秒为单位的最小时间。 感谢 @ToBiChi 提供翻译和 @communist 提供的建议。

Explaination for the first sample  $ t=0 $ 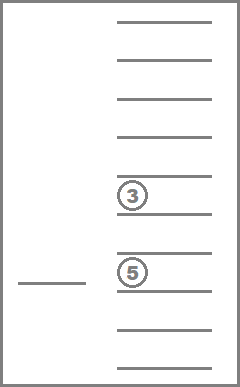 $ t=2 $ 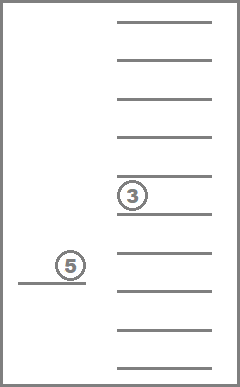 $ t=3 $ 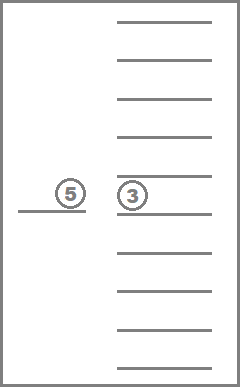 $ t=5 $ 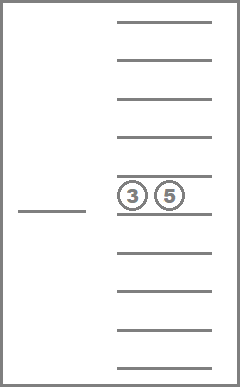 $ t=6 $  $ t=7 $  $ t=9 $  $ t=10 $