CF983D Arkady and Rectangles

Arkady 拥有一张无限大的平面，初始时被涂成颜色 $0$。然后他依次画上 $n$ 个矩形，每个矩形的边都平行于笛卡尔坐标轴，并且完全填充颜色。第 $i$ 个矩形的颜色为 $i$（矩形按照绘制顺序从 $1$ 到 $n$ 编号）。新的矩形可能会完全或部分覆盖之前的矩形。 请你计算在 Arkady 画完所有矩形后，平面上出现了多少种不同的颜色，包括颜色 $0$。

第一行包含一个整数 $n$（$1 \le n \le 100\,000$），表示矩形的数量。 接下来的 $n$ 行中，第 $i$ 行包含 $4$ 个整数 $x_1$、$y_1$、$x_2$ 和 $y_2$（$-10^9 \le x_1 < x_2 \le 10^9$，$-10^9 \le y_1 < y_2 \le 10^9$），表示第 $i$ 个矩形的左下角和右上角坐标。

输出一个整数，表示平面上出现的不同颜色的数量，包括颜色 $0$。

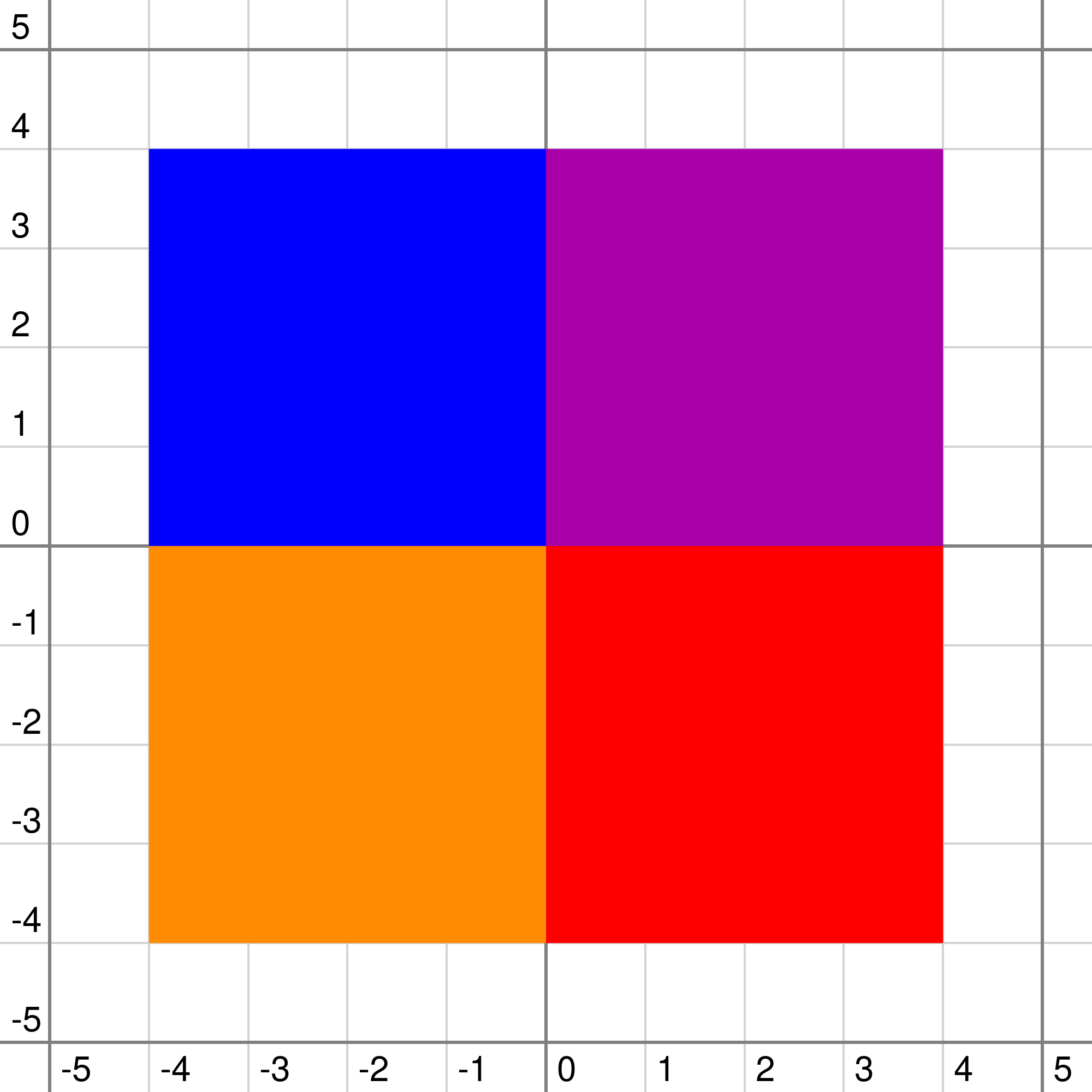 这是第一个样例中平面的样子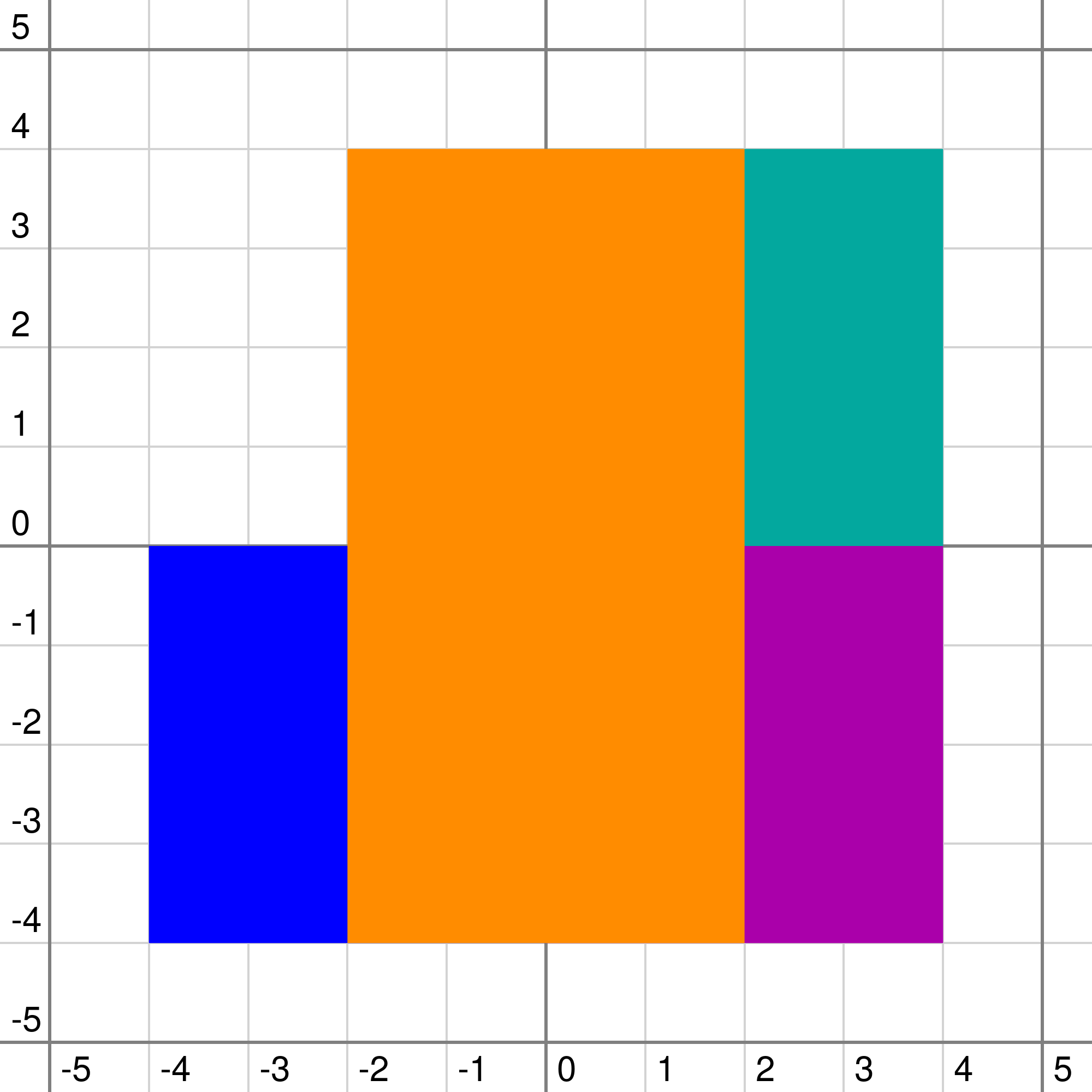！  这是第二个样例中平面的样子。 $0$ = 白色，$1$ = 青色，$2$ = 蓝色，$3$ = 紫色，$4$ = 黄色，$5$ = 红色。 由 ChatGPT 4.1 翻译