CF989E A Trance of Nightfall

清风徐来，流水潺潺。“如此流转逝去，水终究未曾消失；如此盈亏圆缺，月终究未曾增减。” “一切事物既是短暂的，又是永恒的。” Kanno 并不太明白 Mino 这些孤零零的话语，但也许现在正是享受微风与夜空——大自然无尽馈赠的时刻。 仰望繁星点点的夜空，Kanno 沉醉于一夜的安宁美梦。 现在，给定一个包含 $n$ 个点的集合 $S$，这些点位于平面直角坐标系上。 Kanno 可以从平面上的任意一点 $P$ 出发。若 $P$ 不属于 $S$，则 $P$ 不会被加入到 $S$ 中。接下来，Kanno 会重复执行如下操作（统称为一次移动）若干次，操作顺序如下： 1. 选择一条直线 $l$，该直线需经过 $S$ 中至少两个点，并且经过 Kanno 当前所在的位置。如果有多条满足条件的直线，则等概率随机选择一条。 2. 移动到 $S$ 中位于 $l$ 上的某个点。所有可能的目标点（包括当前点本身，如果它属于 $S$）等概率随机选择一个。 现在有 $q$ 个询问，每个询问包含两个整数 $(t_i, m_i)$。对于每个询问，请你帮助 Kanno 选择合适的起点 $P$，使得经过 $m_i$ 次移动后，停留在 $S$ 中第 $t_i$ 个点的概率最大，并输出该最大概率。注意，根据规则 1，$P$ 必须在至少一条经过 $S$ 中至少两个点的直线上。

第一行包含一个正整数 $n$（$2 \leq n \leq 200$），表示 $S$ 中的点的数量。 接下来的 $n$ 行，每行包含两个用空格分隔的整数 $x_i$ 和 $y_i$（$-10^4 \leq x_i, y_i \leq 10^4$），表示 $S$ 中第 $i$ 个点的坐标。保证所有点两两不同。 接下来一行包含一个正整数 $q$（$1 \leq q \leq 200$），表示询问的数量。 接下来的 $q$ 行，每行包含两个用空格分隔的整数 $t$ 和 $m$（$1 \leq t_i \leq n$，$1 \leq m_i \leq 10^4$），分别表示目标点的编号和移动次数。

输出 $q$ 行，每行一个小数，第 $i$ 行表示在第 $i$ 个询问中，经过 $m_i$ 次移动后，停留在 $S$ 中第 $t_i$ 个点的最大概率（通过选择合适的起点 $P$ 得到）。 你的答案如果与标准答案的绝对误差不超过 $10^{-6}$，则视为正确。 形式化地说，设你的答案为 $a$，标准答案为 $b$，只要 $|a - b| \le 10^{-6}$ 即为正确。

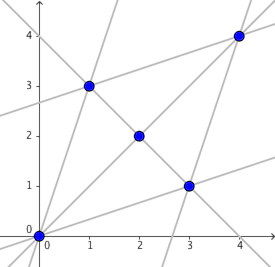
$S$ 中的点和所有可能的直线 $l$ 如下图所示。  对于第一个询问，当 $P = (-1, -3)$ 时，$l$ 唯一确定为 $3x = y$，因此 Kanno 以 $\frac{1}{2}$ 的概率移动到 $(0, 0)$。 对于第三个询问，当 $P = (2, 2)$ 时，$l$ 可能为 $x + y = 4$ 或 $x = y$，等概率选择。Kanno 随后以 $\frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}$ 的概率移动到其他四个点中的任意一个，或者以 $\frac{1}{3}$ 的概率停留在 $(2, 2)$。 由 ChatGPT 4.1 翻译