CF997D Cycles in product

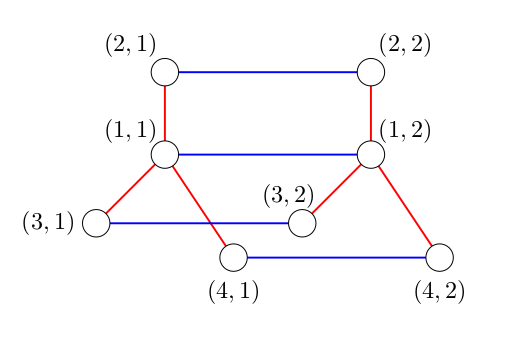
给定一棵树（即无环连通无向图）$T_1$ 和一棵树 $T_2$。我们定义它们的笛卡尔积 $T_1 \times T_2$ 如下： 设 $V$ 是 $T_1$ 的顶点集合，$U$ 是 $T_2$ 的顶点集合。 则图 $T_1 \times T_2$ 的顶点集合为 $V \times U$，即所有有序顶点对的集合，其中第一个顶点来自 $V$，第二个顶点来自 $U$。 我们绘制如下边： - 若 $u_1$ 和 $u_2$ 在 $U$ 中相邻，则在 $(v, u_1)$ 和 $(v, u_2)$ 之间连一条无向边。 - 同理，若 $v_1$ 和 $v_2$ 在 $V$ 中相邻，则在 $(v_1, u)$ 和 $(v_2, u)$ 之间连一条无向边。 关于样例测试中树的积的图片，请参见提示部分。 现在我们考察图 $T_1 \times T_2$。它包含多少个长度为 $k$ 的环（不一定是简单环）？由于答案可能很大，请输出其对 $998244353$ 取模的结果。 顶点序列 $w_1, w_2, \ldots, w_k$，其中 $w_i \in V \times U$，称为一个环，如果任意相邻两个顶点是相邻的，并且 $w_1$ 与 $w_k$ 也相邻。仅仅通过循环移位或遍历方向不同而不同的环，仍然被视为不同的环。

输入的第一行包含三个整数 $n_1$、$n_2$ 和 $k$（$2 \le n_1, n_2 \le 4000$，$2 \le k \le 75$），分别表示第一棵树的顶点数、第二棵树的顶点数和环的长度。 接下来 $n_1 - 1$ 行描述第一棵树。每行包含两个整数 $v_i, u_i$（$1 \le v_i, u_i \le n_1$），表示一条边。 接下来 $n_2 - 1$ 行描述第二棵树，格式相同。 保证给定的图都是树。

输出一个整数，表示环的数量，对 $998244353$ 取模。

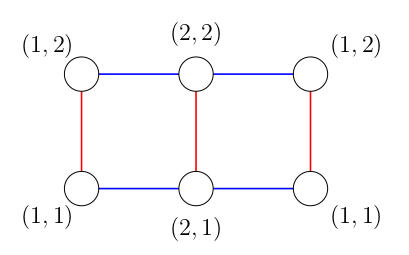
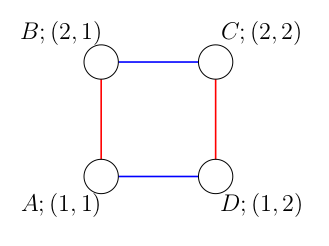
下列三幅图片展示了样例测试中树的积所对应的图。 在第一个样例中，长度为 $2$ 的环的列表如下： - «AB», «BA» - «BC», «CB» - «AD», «DA» - «CD», «DC»  由 ChatGPT 4.1 翻译