CF999E Reachability from the Capital
题目描述
在 Berland 有 $n$ 座城市和 $m$ 条道路,每条道路连接着一对城市。
Berland 的道路都是**单向**的
为了能让首都能够到达所有的城市,最少需要新修建多少新道路?
新道路也是单向的
输入格式
输入的第一行包含三个整数 $n,m$ 和 $s$ $(1\le n \le 5000,0\le m \le 5000 , 1\le s \le n)$ ——城市数,道路数和首都所在城市的标号。 城市的标号为 $1$ \~ $n$
接下来 $m$ 行每行包含一条道路连接着一对城市 $u_i,v_i$ $(1\le u_i,v_i\le n,u_i\ne v_i)$
对于每对城市 $u,v$,从 $u$ 到 $v$ 最多只能有一条道路。 允许在一对城市之间建造相反方向的道路(即从 $u$ 到 $v$ 和从 $v$ 到 $u$ )。
输出格式
输出一个整数——使从首都可以到达所有城市所需的最少新修建道路数。如果从 $s$ 已经可以到达所有城市,则输出 $0$。
说明/提示
样例 1:
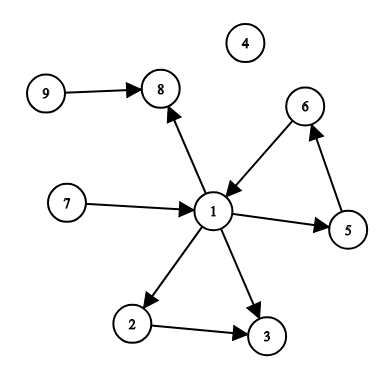
例如,您可以添加道路 ( 6, 4 ) , ( 7 , 9 ) , ( 1 , 7 ),以使从 $s = 1$ 可到达所有城市。
样例 2:
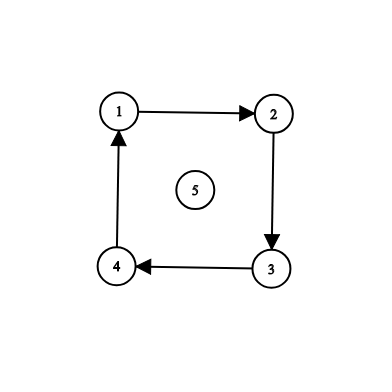
在此样例中,您可以添加道路(5 , 1),(5 , 2),(5 , 3),(5 , 4)中的任何一条,以使可从 $s = 5$ 到达所有城市。