P10003 [集训队互测 2023] 傅里叶与交通系统

傅里叶荣升巴黎市交通部长。新官上任三把火，傅里叶决定重构巴黎市的交通系统。

巴黎市的地图可以看成一个无限大的二维平面。傅里叶在上面修建了 $n$ 条传送带：第 $i$ 条传送带修建于 $x\in[p_{i-1},p_i),y\in\mathbb R$ 的区域中。对于 $x

第一行三个整数 $n,q,V$，表示传送带数目、询问个数以及人的移动速度。 下一行 $n+1$ 个整数 $p_0,p_1,\dots,p_n$，表示传送带的边界信息。 下一行 $n$ 个整数 $v_1,v_2,\dots,v_n$，表示每个传送带的速率。 接下来 $q$ 行，每行四个整数 $x_1,y_1,x_2,y_2$，表示此次询问的起讫点。

对于每次询问，输出一行一个实数，表示此次移动所需的最小时长，单位为秒。你需要保证输出与标准答案的相对或绝对误差不超过 $10^{-5}$。 - 如果你怀疑你的代码中出现了较大的精度误差，可以尝试使用更多整数和分数以规避浮点数运算，从而减少误差。

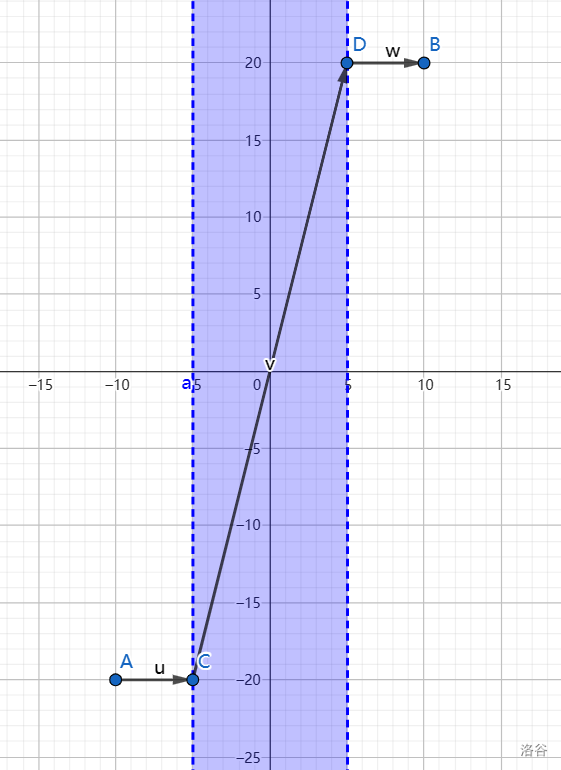
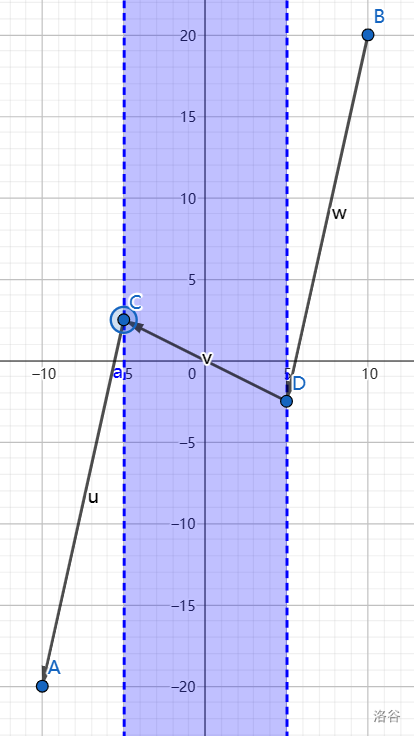
样例 #4，#5 详见附件。 ------------ 样例 #1 的解释：  第一问中，上图是一种极优的行走方式。蓝色区域是传送带所在区域，在其上时我们以 $(3,12)$ 每秒的速度移动（其中自身移动的速度是 $(3,7)$，也即可以看作是三成时间沿着 $x$ 轴正方向、七成时间沿着 $y$ 轴正方向移动；在极短时间内不停切换，可以达成如上图中斜线行走的效果；$(3,7)$ 的自身行走与 $(0,5)$ 的传送带运转叠加成为 $(3,12)$ 的速度向量）。  第二问中，上图是一种极优的行走方案。 需要注意的是，这两问中能达成最少时间的行走方案不止图中给出的两种。 对于所有数据，均满足 $n,q\leq1.5\times10^5$，$-5\times10^5\leq p_0