P1002 [NOIP 2002 Junior] River-Crossing Pawn

On a chessboard, there is a river-crossing pawn at point $A$ that needs to reach the target point $B$. The pawn moves according to the rules: it may move either downward or rightward. There is also an opposing knight at point $C$ on the board; the knight’s own square and all squares reachable by a single knight move are called the knight’s controlled squares. Therefore, this is called “the knight blocks the river-crossing pawn.” The board is represented using coordinates: point $A$ is at $(0, 0)$, point $B$ is at $(n, m)$, and the knight’s position is also given.  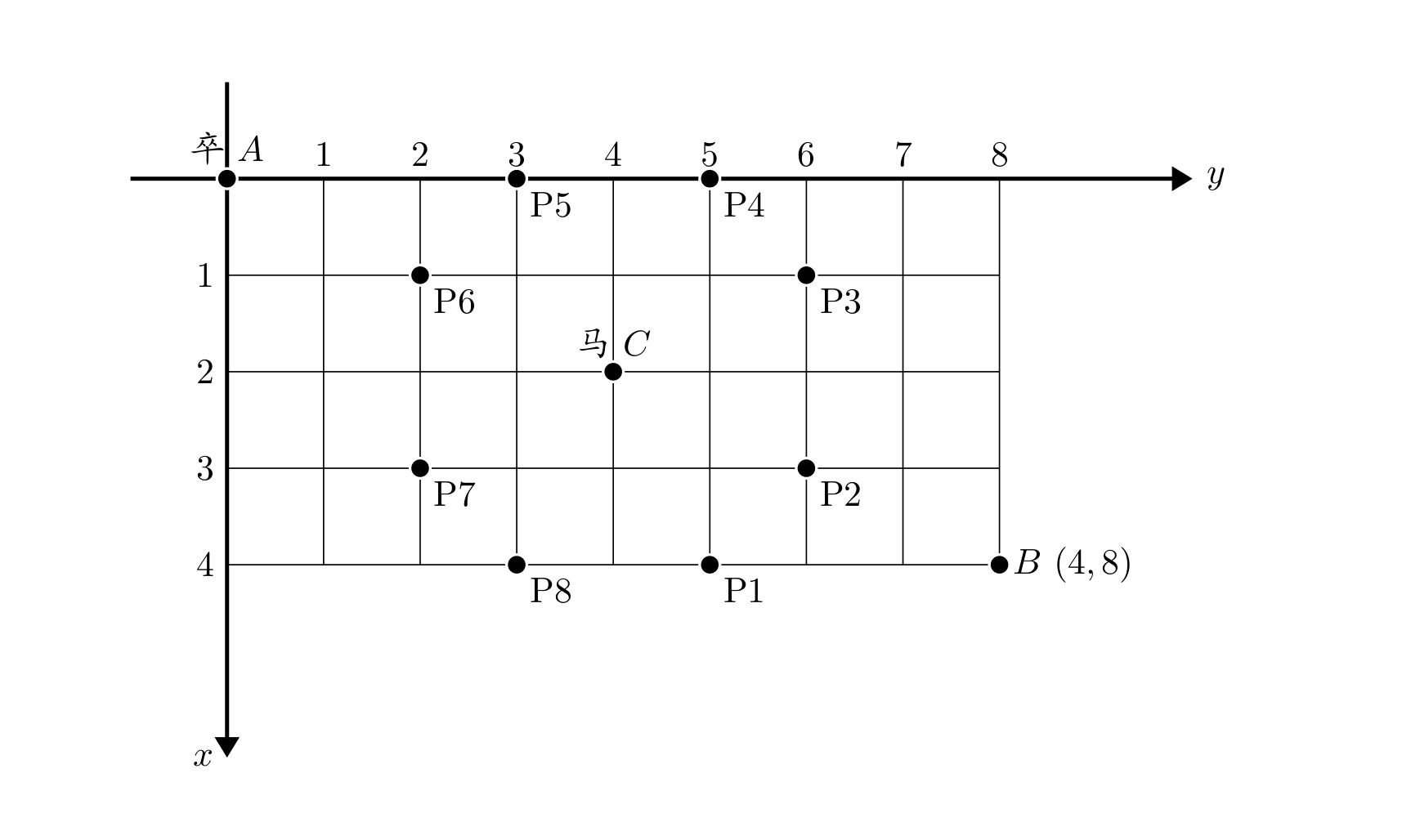You are to compute the number of distinct paths by which the pawn can travel from point $A$ to point $B$, assuming the knight’s position is fixed and does not move in response to the pawn’s moves.

One line contains four integers, representing the coordinates of point $B$ and the coordinates of the knight, in order: $n$, $m$, $x$, $y$.

Output a single integer, the total number of valid paths.

For $100\%$ of the data, $1 \le n, m \le 20$, and the knight’s coordinates satisfy $0 \le x, y \le 20$. [Source] NOIP 2002 Junior, Problem 4. Translated by ChatGPT 5