P1003 [NOIP 2011 Senior] Laying Carpets

To prepare a unique awards ceremony, the organizers lay several rectangular carpets on a rectangular area of the venue (regarded as the first quadrant of the plane Cartesian coordinate system). There are $n$ carpets, numbered from $1$ to $n$. These carpets are laid, in increasing order of their indices, axis-parallel; a later carpet is placed on top of those already laid. After all carpets have been laid, the organizers want to know the index of the topmost carpet that covers a given point on the floor. Note: points on the boundary and at the four vertices of a rectangular carpet are also considered covered.

The input contains $n + 2$ lines. The first line contains an integer $n$, indicating that there are $n$ carpets in total. Each of the next $n$ lines, the $(i+1)$-th line, describes carpet $i$ with four integers $a, b, g, k$, separated by single spaces, representing the coordinates of the lower-left corner $(a, b)$ and the lengths of the carpet in the $x$- and $y$-directions, respectively. The $(n + 2)$-th line contains two integers $x$ and $y$, representing the coordinates $(x, y)$ of the query point.

Output a single line containing one integer, the index of the required carpet; if the point is not covered by any carpet, output `-1`.

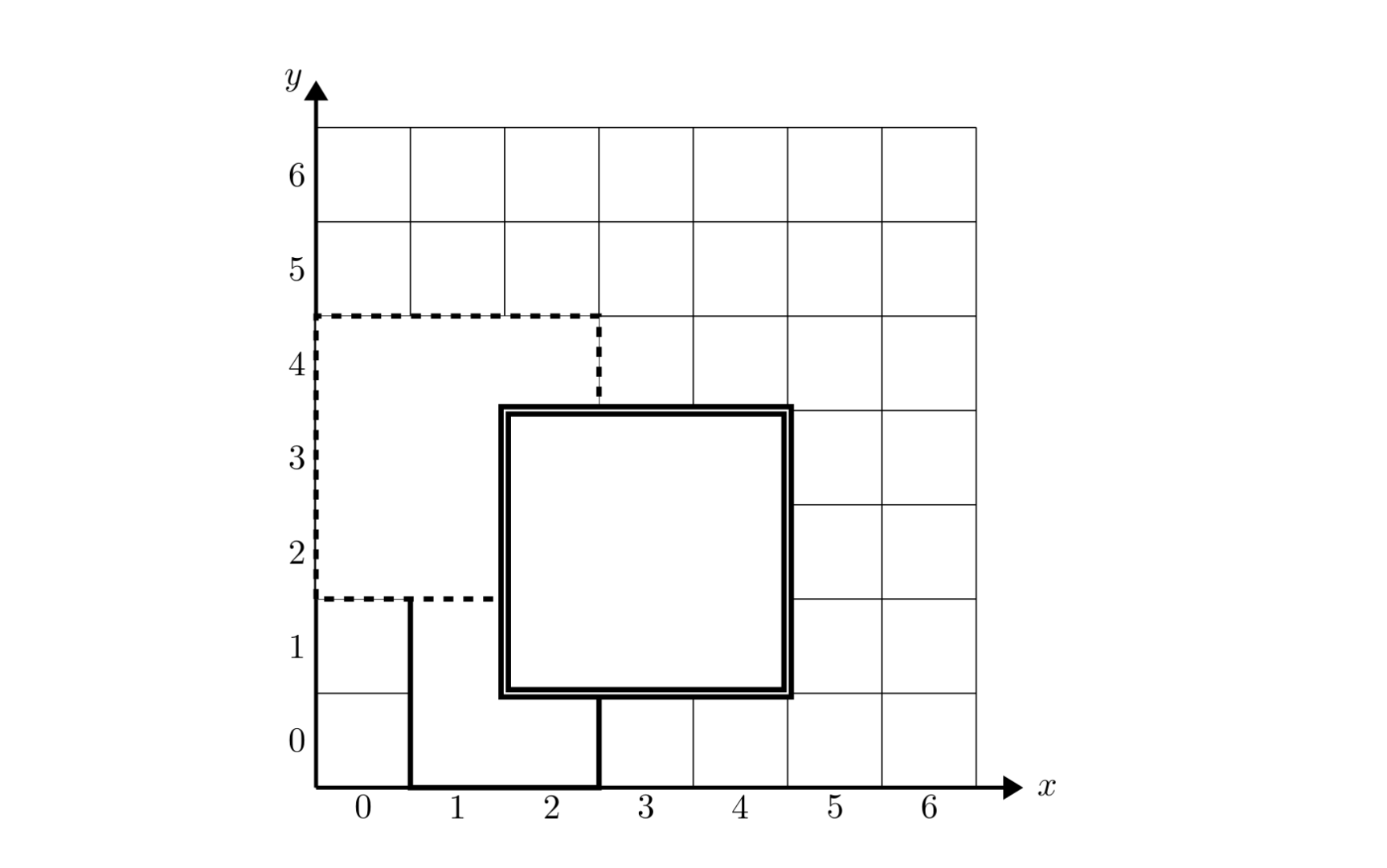
[Sample Explanation 1] As shown in the figure, carpet $1$ is drawn with solid lines, carpet $2$ with dashed lines, and carpet $3$ with double solid lines. The topmost carpet covering the point $(2, 2)$ is carpet $3$.  [Data Range] - For $30\%$ of the data, $n \le 2$. - For $50\%$ of the data, $0 \le a, b, g, k \le 100$. - For $100\%$ of the data, $0 \le n \le 10^4$, $0 \le a, b, g, k \le 10^5$. NOIP 2011 Senior Day 1 Problem $1$. Translated by ChatGPT 5