P10097 [ROIR 2023] 彩点 (Day 1)

翻译自 [ROIR 2023 D1T4](https://neerc.ifmo.ru/school/archive/2022-2023/ru-olymp-regional-2023-day1.pdf)。 平面上有 $n$ 个点，分别是 $P_1,P_2,P_3,\dots，P_n$。第 $i$ 个点的坐标为 $(x_i,y_i)$。 选择两个点 $P_i,P_j$（$i\ne j$）。设 $P_i$ 为起始点，$P_j$ 为终止点。**以终止点 $P_j$ 为中心**，从向量 $\overrightarrow{P_iP_j}$ **的方向**开始按照逆时针顺序将除 $P_j$ 以外的点进行排序（角度相同时按照到点 $P_j$ 的距离升序排序）。假设排序后的第 $t$ 个点为 $P_k$，则继续重复操作，设 $P_j$ 为起始点，$P_k$ 为终止点，按照相同的方法重新排序并计算新的终止点的编号。这个过程循环进行。 在下图中，刚开始时 $n=6,t=4,i=1,j=2$。按照顺序将除了 $P_2$ 以外的点排序，结果是 $P_3,P_5,P_1,P_6,P_4$，所以下一个终止点应该是 $P_6$，起始点是 $P_2$。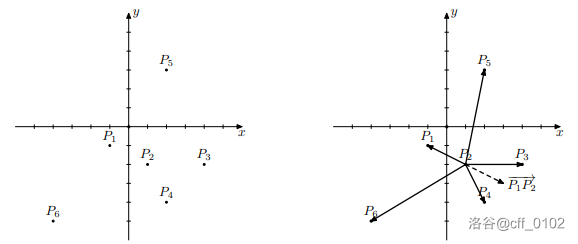  此时 $n=6,t=4,i=2,j=6$。继续按照规则排序，如左下图，结果是 $P_4,P_3,P_2,P_1,P_5$。所以下一个终止点是 $P_1$，起始点是 $P_6$。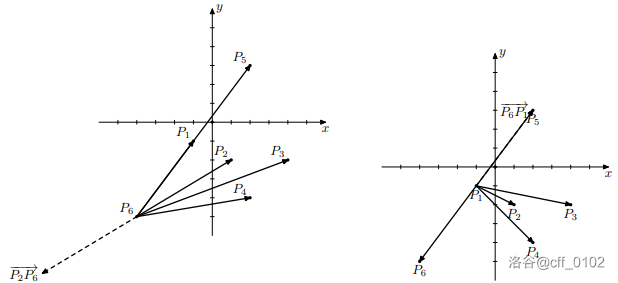  此时 $n=6,t=4,i=6,j=1$。继续按照规则排序，如右上图，结果是 $P_5,P_6,P_4,P_2,P_3$。所以下一个终止点是 $P_2$，起始点是 $P_1$。此时就回到刚开始的情况，进入了一个循环。

我们将 $n$ 个点中的每个点涂上三种颜色之一。第 $i$ 个点的颜色如下确定： - 如果存在点 $j$，选取点 $i$ 作为起始点，点 $j$ 作为终止点，在上面的过程中点 $i$ 会无数次成为起始点，则将点 $i$ 涂成绿色。 - 如果点 $i$ 没有涂成绿色并且存在点 $j$，选取点 $i$ 作为起始点，点 $j$ 作为终止点，在上面的过程中点 $i$ 至少还能成为起始点一次，则将点 $i$ 涂成蓝色。 - 如果点 $i$ 既不是绿色也不是蓝色，则将点 $i$ 涂成红色。 对于每个点，确定它应该涂成哪种颜色。

第一行包含两个整数 $n$ 和 $t$。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$。保证没有两个点重合。

输出一行，包含 $n$ 个字符，字符串的第 $i$ 个字符表示第 $i$ 个点的颜色。 绿色点用字母 `G` 表示，蓝色点用字母 `B` 表示，红色点用字母 `R` 表示。

样例 $1$ 解释： 在前面举的例子中已经知道 $P_1,P_2,P_6$ 构成一个循环，这三个点肯定会被无限次访问，所以应被涂上绿色。 当起始点是 $P_3$ 时，可以令终止点为 $P_1$，排序后 $P_3$ 正好是第四个，这样 $P_3$ 就重回起始点了，如下图。所以应该涂蓝。  当起始点是 $P_4$ 时，可以选择 $P_5$ 为终止点，排序后 $P_4$ 正好是第四个。所以 $P_4$ 可以涂蓝。当 $P_5$ 是起始点时，易得它既不能被涂上绿色也不能被涂上蓝色，所以涂红。 本题使用捆绑测试。 | 子任务 | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $10$ | $n\le10$，所有点共线 | | $2$ | $15$ | 所有点共线 | | $3$ | $10$ | $n\le10$，没有蓝色点 | | $4$ | $10$ | $n\le10$ | | $5$ | $15$ | $n\le100$，没有蓝色点 | | $6$ | $15$ | $n\le100$ | | $7$ | $5$ | $n\ge3$，所有点构成一个严格凸 $n$ 边形，且按照逆时针顺序输入 | | $8$ | $20$ | 无 | 对于全部数据，$2 \le n \le 1 000, 1 \le t \le n−1,−10^9 \le x_i, y_i \le 10^9$。