『STA - R4』踱步

小 X 特别喜欢安静的环境，因为那可以让他心情愉悦。 现在给出 $N$ 分钟内每分钟屋内和屋外对小 X 的心情影响值，在这 $N$ 分钟内，小 X 可以从屋内踱步到屋外或是从屋外踱步到屋内**最多共** $K$ 次。（小 X 当且仅当每分钟初进行踱步，同一时刻至多踱步一次，并且踱步的时间忽略不计。第 $1$ 分钟初不可踱步，第 $N$ 分钟初可以踱步。但是在第 $1$ 分钟初可以自由选择初始状态）。 同时，过于频繁的改变会让小 X 心情烦躁，所以如果两次踱步的间隔**小于等于** $T$ 分钟，会对小 X 的心情额外造成 $P$ 点影响。（如果此次踱步是在第 $t_a$ 分钟初，上一次踱步是在第 $t_b$ 分钟初，那么这两次踱步的时间间隔为 $t_a - t_b$ 分钟）。 小 X 想知道自己的心情最好可以是多少，即第 $N$ 分钟末小 X 心情值的最大值。 若某一时刻小 X 的心情值为 $a$，之后小 X 的心情被影响了 $b$，那么在此之后小 X 的心情值将变为 $a + b$。

**本题单个测试点内含有多组测试数据。** 第一行两个正整数 $\text{id},\text{TEST}$。其中 $\text{id}$ 代表 Subtask 编号，$\text{TEST}$ 代表测试数据组数。特别的，样例的 $\text{id}$ 为 $0$。 对于每组测试数据： 第一行为四个整数 $N, K, T, P$。 接下来 $N$ 行每行两个整数。其中第 $i$ 行的两个整数 $a_i, b_i$ 分别代表第 $i$ 分钟屋内和屋外对小 X 心情的影响值。

对于每组测试数据，输出一行一个整数，代表第 $N$ 分钟末小 X 心情值的最大值。

0 2
8 3 2 3
0 -2
5 -10
8 0
-10 -7
0 -3
-4 -9
-9 -3
-7 0
8 3 2 -6
9 6
9 -6
3 7
-4 3
8 -9
6 0
-10 9
-8 -4

5
36

0 1
12 3 2 -35771156
797235777 25138038
801541087 -405462832
936777370 -973167834
74493410 60154946
263320806 782480907
-940214410 805511853
806065179 463119365
-295177485 -112301429
-403964212 202831413
122359196 611468120
-555210139 549749508
793784715 -38433603

6706692096

0 1
5 2 1 -100
-44 -72
-36 -23
-4 0
-22 -1
-88 3

-65

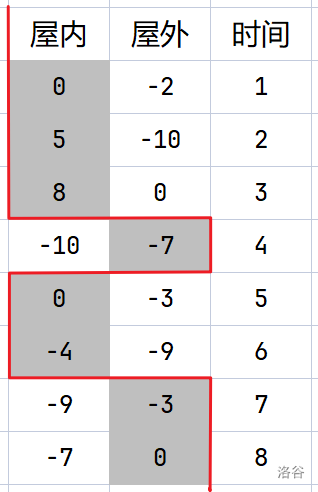
**【样例 #1 解释】** 对于第 $1$ 组数据，最优方案为初始时选择在屋内，分别在第 $4, 5, 7$ 分钟初进行踱步。  其中第 $2$ 次踱步与第 $1$ 次踱步之间的间隔为 $5 - 4 = 1$ 分钟，对小 $\text{X}$ 的心情产生 $3$ 的贡献，第 $3$ 次踱步与第 $2$ 次踱步之间的间隔为 $7 - 5 = 2$ 分钟，对小 X 的心情产生 $3$ 的贡献。 因此小 X 的心情值为 $$\left(0+5+8-7+0-4-3+0\right) + 6 = 5$$ 前半部分为灰色格子的权值和，后半部分为两次频繁踱步产生的额外贡献，可以证明此方案最优。 **【样例 #2 解释】** 请注意答案可能超过 $32$ 位整型数字的范围。 **【样例 #3 解释】** 请注意答案可能为负数。 **【数据范围】** 对于 $100\%$ 的数据： - $1 \le \text{TEST} \le 10^5$； - $2 \le N \le 2 \times 10^5$； - $1 \le K \le \min\left\{200, N\right\}$； - $1 \le T \le \min\left\{2 \times 10^4, N\right\}$； - $\left\lvert a_i \right\rvert,\left\lvert b_i \right\rvert,\left\lvert P \right\rvert \le 10^9$。 - $\sum N \cdot K \le 5 \times 10^7$。 - 保证单个测试点输入数据规模不超过 10 MB。 **本题采用捆绑测试。** |Subtask 编号|数据范围|分值|依赖子任务| |:--------:|:--------:|:--------:|:--------:| |1|$N \le 20, \text{TEST} \le 10$|$5$|| |2|$\sum N^2K \le 5 \times 10^7$|$20$|$1$| |3|$K \le 5, N \le 5 \times 10^4, \text{TEST} \le 10$|$15$|| |4|$P=-10^9, 0 \le \left\lvert a_i \right\rvert,\left\lvert b_i \right\rvert \le 100$|$30$|| |5|无特殊限制|$30$|$1,2,3,4$|