P10225 [COCI 2023/2024 #3] Milano C.le

**译自 [COCI 2023/2024 Contest #3](https://hsin.hr/coci/archive/2023_2024) T3「[Milano C.le](https://hsin.hr/coci/archive/2023_2024/contest3_tasks.pdf)」**

Silvia 目前在米兰中央车站，她注意到车站有很多站台。她觉得站台数量太多了，所以她打算统计有多少真正需要的站台。 Silvia 同样注意到这个车站的一个有趣的事实：出发和到达时刻表每两天就会重复一次，并且时刻表满足所有 $n$ 列火车在一天到达车站，并且在另一天离开。注意按这种方式，没有火车会在所有火车都到达之前离开。 车站的站台足够长，可以满足所有 $n$ 列火车都能在同一站台停成一列。然而，如果火车 $x$ 先进入站台，然后 $y$ 进入同一站台，则火车 $x$ 不可以在火车 $y$ 离开站台之前离开。 Silvia 想知道在不存在由于排在某列火车前面的火车还没离开导致这列火车无法离开的情况下，最少需要多少站台可以使所有火车都停下。

第一行一个整数 $n\ (1\le n\le 2\cdot 10^5)$，表示火车的数量。 第二行包含 $n$ 个整数 $a_i\ (1\le a_i\le n,\forall i\neq j,a_i\neq a_j)$，表示第 $i$ 列火车在第一天第 $a_i$ 个到达车站。序列 $(a_i)$ 是一个排列。 第三行包含 $n$ 个整数 $b_i\ (1\le b_i\le n,\forall i\neq j,b_i\neq b_j)$，表示第 $i$ 列火车在第二天第 $b_i$ 个离开车站。序列 $(b_i)$ 是一个排列。

输出一行一个整数，表示最少需要多少个站台。

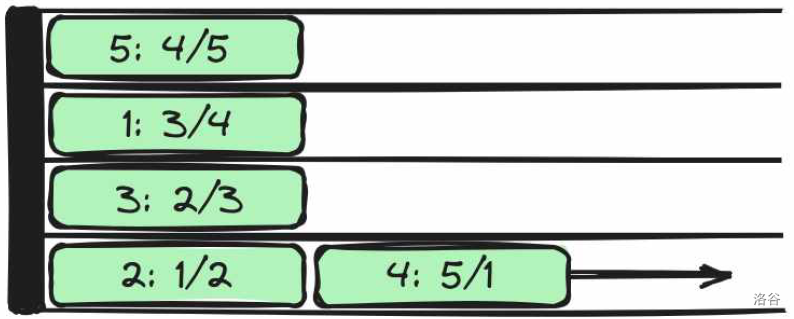
### 样例解释 2  上图展示了一个样例二中站台上可能的列车调度情况。列车上 $(i:a_i/b_i)$ 的标签表示第 $i$ 列火车在第一天第 $a_i$ 个到达车站，然后在第二天第 $b_i$ 个离开车站。火车 $(2:1/2)$ 不能比火车 $(4:5/1)$ 更早离开车站。 ### 样例解释 3 所有火车均可在同一站台排成一列，没有任何问题。 ### 子任务 | 子任务 | 附加限制 | 分值 | | :--------: | :----------------------------------: | :--: | | $1$ | $n\le 10$ | $21$ | | $2$ | 最小所需站台数要么是 $1$，要么是 $2$ | $18$ | | $3$ | $n\le 1\ 000$ | $31$ | | $4$ | 无附加限制 | $40$ |