P1023 [NOIP 2000 Junior] Taxation and Subsidy Problem

每样商品的价格越低，其销量就会相应增大。现已知某种商品的成本及其在若干价位上的销量（产品不会低于成本销售），并假设相邻价位间销量的变化是线性的且在价格高于给定的最高价位后，销量以某固定数值递减。（我们假设价格及销售量都是整数） 对于某些特殊商品，不可能完全由市场去调节其价格。这时候就需要政府以税收或补贴的方式来控制。（所谓税收或补贴就是对于每个产品收取或给予生产厂家固定金额的货币）

You are a project manager at a consulting firm. You already know the government's expected price for a certain product, as well as its sales at various price points. You are required to determine the minimum amount (also an integer) of tax to collect or subsidy to grant on this product so that, at the government's expected price, the seller achieves the maximum total profit compared with all other price points. - Total profit $=$ profit per unit $\times$ sales. - Profit per unit $=$ unit price $-$ unit cost (minus tax or plus subsidy).

- The first line is the government's expected price for the product. - The second line contains two integers: the first is the product's cost, and the second is the sales volume when sold at cost price. - Then follow several lines, each containing two integers: the first is the unit price at some price point, and the second is the sales volume at that price. A line `-1 -1` indicates that all known price points and their corresponding sales have been entered. - The last line contains a single integer indicating the decrease in sales for each 1 yuan increase in price beyond the highest known unit price.

There are two cases: - If the maximum total profit can be achieved at the government's expected price, output a single integer. Its sign indicates whether it is a subsidy or a tax, and its absolute value is the minimum amount. If there are multiple solutions, output the one with the smallest absolute value. - If the maximum total profit cannot be achieved at the government's expected price, output `NO SOLUTION`.

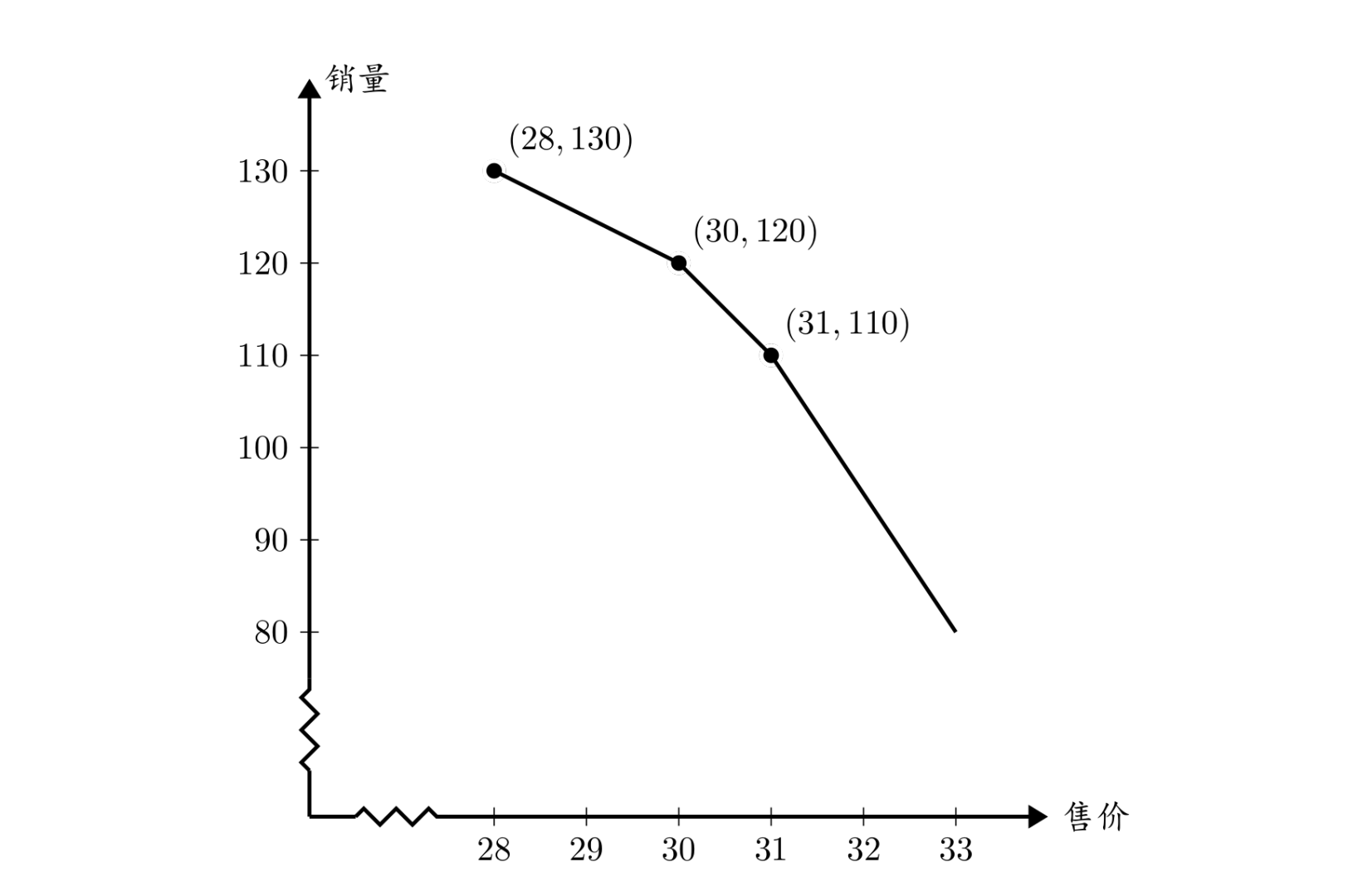
### Constraints and Conventions All input numbers are less than $10^5$. ### Sample Explanation (updated on 2023/6/22) The following figure shows the price–sales curve corresponding to the sample input. The horizontal axis represents the selling price, and the vertical axis represents the sales volume.  According to the problem statement, the cost is $28$ yuan. The selling price should not be lower than $28$ yuan. When the selling price exceeds the maximum given price $31$ yuan, the sales decrease by $15$ for each 1 yuan increase in price. For example, when the selling price is $33$ yuan, the sales are $110-15\times (33-31)=80$. Between the given price points, the sales change linearly. When the government provides a subsidy of $4$ yuan for this product and the firm sets the price at $31$ yuan, the profit is $31-28+4=7$ yuan per unit, the sales are $110$ units, and the total profit is $7\times 110=770$ yuan, which is the maximum total profit the firm can obtain among all pricing choices. In this case, the firm's selling price matches the government's expected price, so this is a valid solution. Translated by ChatGPT 5