P1027 [NOIP 2001 Senior] Car's Travel Route

It is summer vacation again. Car, who lives in city A, wants to travel with her friends. She knows that each city has $4$ airports located at the $4$ vertices of a rectangle. Between any two airports within the same city, there is a straight high-speed railway; in the $i$-th city, the unit distance cost of the high-speed railway is $T_i$. Between any two airports in different cities, there is a flight route, and the unit distance cost of all flight routes is $t$.  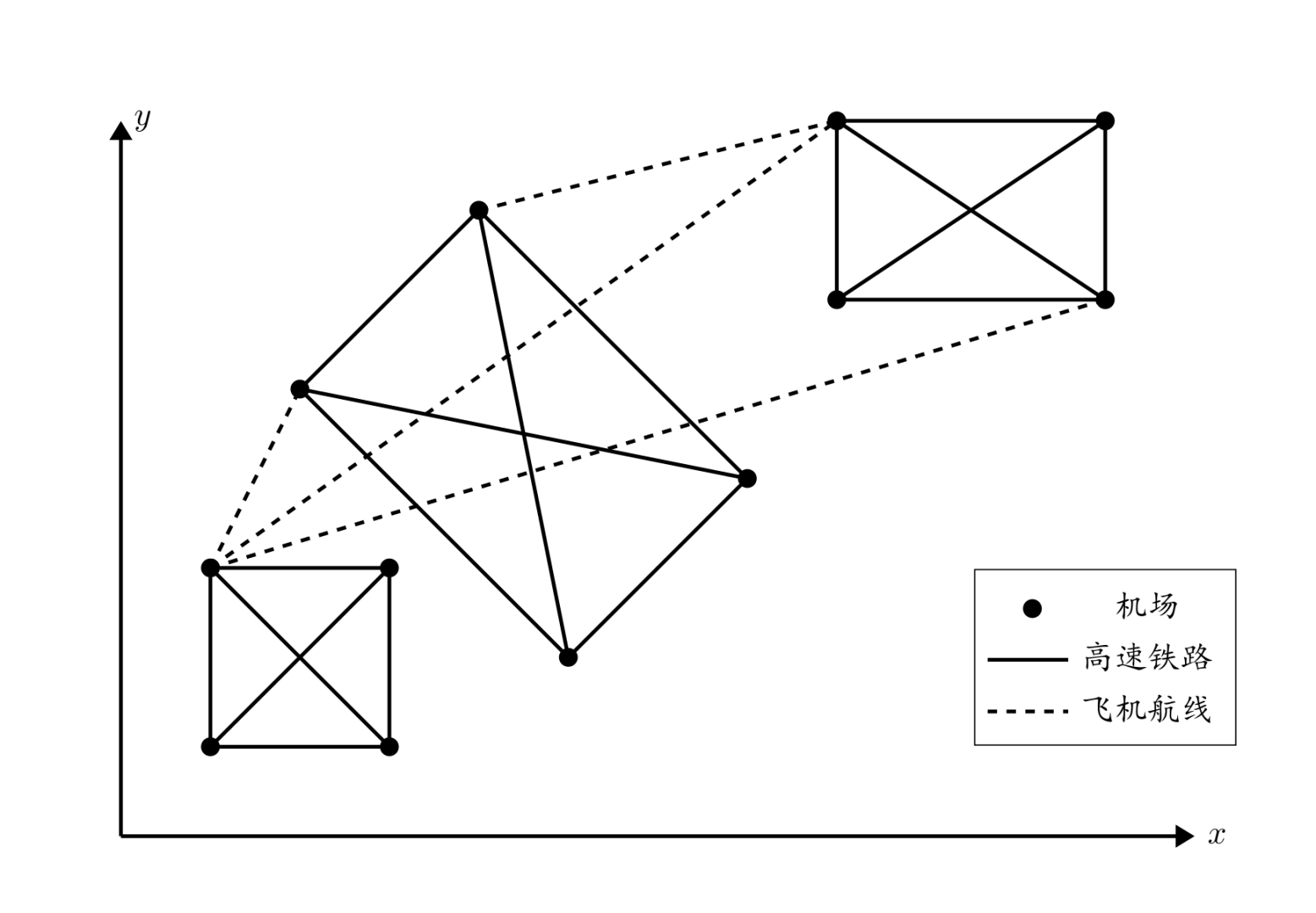Note: The figure does not show all railways and flight routes. How should Car plan her route to city B to minimize the expense? She finds this is not a simple problem and asks you for help. Find a travel route from city A to city B. The departure and arrival airports within their respective cities can be chosen arbitrarily. Minimize the total cost.

The first line contains a positive integer $n$, the number of test cases. For each test case: - The first line contains $4$ positive integers $S, t, A, B$. - $S$ is the number of cities. - $t$ is the unit distance cost for flights. - $A$ and $B$ are the indices of city A and city B, respectively. - The next $S$ lines each contain $7$ positive integers $x_{i1}, y_{i1}, x_{i2}, y_{i2}, x_{i3}, y_{i3}, T_i$. Here $(x_{i1}, y_{i1})$, $(x_{i2}, y_{i2})$, and $(x_{i3}, y_{i3})$ are the coordinates of any $3$ airports in the $i$-th city, and $T_i$ is the unit distance cost of the high-speed railway in the $i$-th city.

Output $n$ lines, one value per test case. Round to one decimal place.

Constraints For $100\%$ of the testdata, $1 \le n \le 10$, $1 \le S \le 100$, $1 \le A, B \le S$, $0 \le t, x_{i1}, y_{i1}, x_{i2}, y_{i2}, x_{i3}, y_{i3}, T_i \le 500$. Source NOIP 2001 Senior, Problem 4. Translated by ChatGPT 5