P10295 [CCC 2024 S1] Hat Circle

在最近的一次聚会上，$N$ 个人围坐在一张圆桌旁，其中 $N$ 是偶数。座椅按顺时针方向编号为 $1\sim N$。每个人都戴着一顶写有数字的帽子。具体来说，座位 $i$ 上的人戴着一个写有数字 $H_i$ 的帽子。 每个人都看着圆圈中与自己正对面的人。 请你求出看到戴着与自己相同号码的帽子的人的数量。

输入的第一行包含一个正偶数 $N$ 表示聚会的人数。 接下来 $N$ 行分别包含一个非负整数 $H_i$，表示第 $i$ 个人的帽子上写的数字。

输出一个整数，表示看到戴着与自己相同号码的帽子的人的数量。

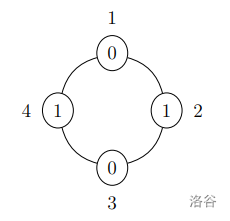
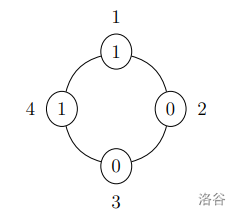
**【样例 1 解释】** 桌子周围的四个座位排布如下图所示。圆圈里的数字表示这个人的帽子上写的数字，圆圈旁边的数字表示这个人的编号。注意每个人看到的数都与自己的帽子上的数相等。坐在位置 $1$ 和 $3$ 上的人都看到了数字 $0$，坐在位置 $2$ 和 $4$ 上的人都看到了数字 $1$。  **【样例 2 解释】** 桌子周围的四个座位排布如下图所示。圆圈里的数字表示这个人的帽子上写的数字，圆圈旁边的数字表示这个人的编号。注意每个人看到的数都不与自己的帽子上的数相等。坐在位置 $1$ 和 $4$ 上的人都看到了数字 $0$，坐在位置 $2$ 和 $3$ 上的人都看到了数字 $1$。  **【数据范围】** **本题采用捆绑测试。** 对于所有数据，保证 $1\leq N\leq 10^6$，$0\leq H_i\leq 2\times 10^6$。 下面的表格显示了 $15$ 分的分配方案： | 分值 | 描述 | $N$ 的范围 | $H_i$ 的范围 | | :-: | :- | :-: | :-: | | $2$ | 人数很少；只有两种可能的帽子上的数 | $N \leq 4$ | $H_i \leq 1$ | | $1$ | 只有一种可能的帽子上的数 | $N \leq 100$ | $H_i = 1$ | | $2$ | 坐在奇数位置上的人的帽子上数为 $1$，坐在偶数位置上的人的帽子上数为 $0$ | $N \leq 100$ | $H_i \leq 1$ | | $5$ | 中等多少的人数 | $N \leq 2 \times 10^3$ | $H_i \leq 4 \times 10^3$ | | $5$ | 很多人和可能的帽子上的数 | $N \leq 10^6$ | $H_i \leq 2 \times 10^6$ |