P1034 [NOIP 2002 Senior] Rectangle Covering

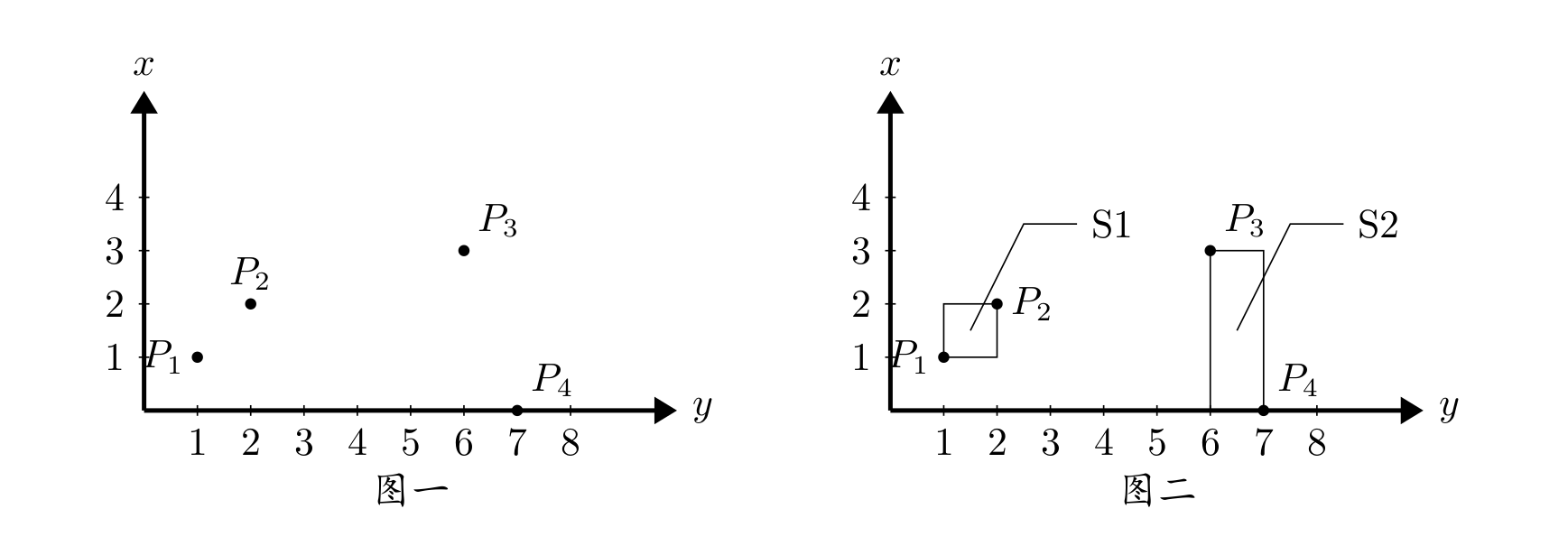
On the plane, there are $n$ points, each represented by a pair of integer coordinates. For example, when $n=4$, the coordinates of the 4 points are $p_1(1,1)$, $p_2(2,2)$, $p_3(3,6)$, $p_4(0,7)$; see Figure 1.  These points can be fully covered by $k$ rectangles whose sides are parallel to the coordinate axes. When $k=2$, two rectangles $s_1, s_2$ as in Figure 2 can cover them, and the sum of their areas is $4$. Given the $n$ points and $k$, how can we make the sum of the areas of the $k$ rectangles that cover all points as small as possible? Conventions: A rectangle covering a single point has area $0$; a rectangle that degenerates to a line segment parallel to a coordinate axis also has area $0$. The rectangles must be pairwise disjoint; they may not overlap or even touch (edges and vertices may not coincide).

The first line contains two integers $n, k$, as described above. The next $n$ lines each contain two integers $x_i, y_i$, where the $(i+1)$-th line gives the coordinates of the $i$-th point.

Output a single integer: the minimum possible sum of the areas of the $k$ rectangles that satisfy the conditions.

For $100\%$ of the testdata, $1 \le n \le 50$, $1 \le k \le 4$, $0 \le x_i, y_i \le 500$. Source: NOIP 2002 Senior, Problem 4. Translated by ChatGPT 5