P10365 [PA 2024] Kraniki

PA 2024 5B2

**题目译自 [PA 2024](https://sio2.mimuw.edu.pl/c/pa-2024-1/dashboard/) Runda 5 [Kraniki](https://sio2.mimuw.edu.pl/c/pa-2024-1/p/kra/)** *Radek and Friends* 公司的负责人 Radek 试图淹没竞争对手 *Mati and Company* 公司的所有货架。为了进行完美的破坏，他让他的朋友，水管工 Janusz 在每个架子都上安装了小水龙头。 为简单起见，*Mati and Company* 公司中的货架可以用平面上的线段来表示。每个货架都是一对点 $(l_i,h_i)$ 和 $(r_i,h_i)$ 之间的线段。水管工安装的水龙头是坐标为 $(\frac{l_i+r_i}{2}, h_i + 0.5)$ 的点。这个房间的地面用 $OX$ 轴表示。 只要打开第 $i$ 个货架上方的水龙头，该货架就会被水淹没。之后水会自然开始从货架的两端垂直向下滴落，并有可能淹没更多的货架，或自然滴落到地面上。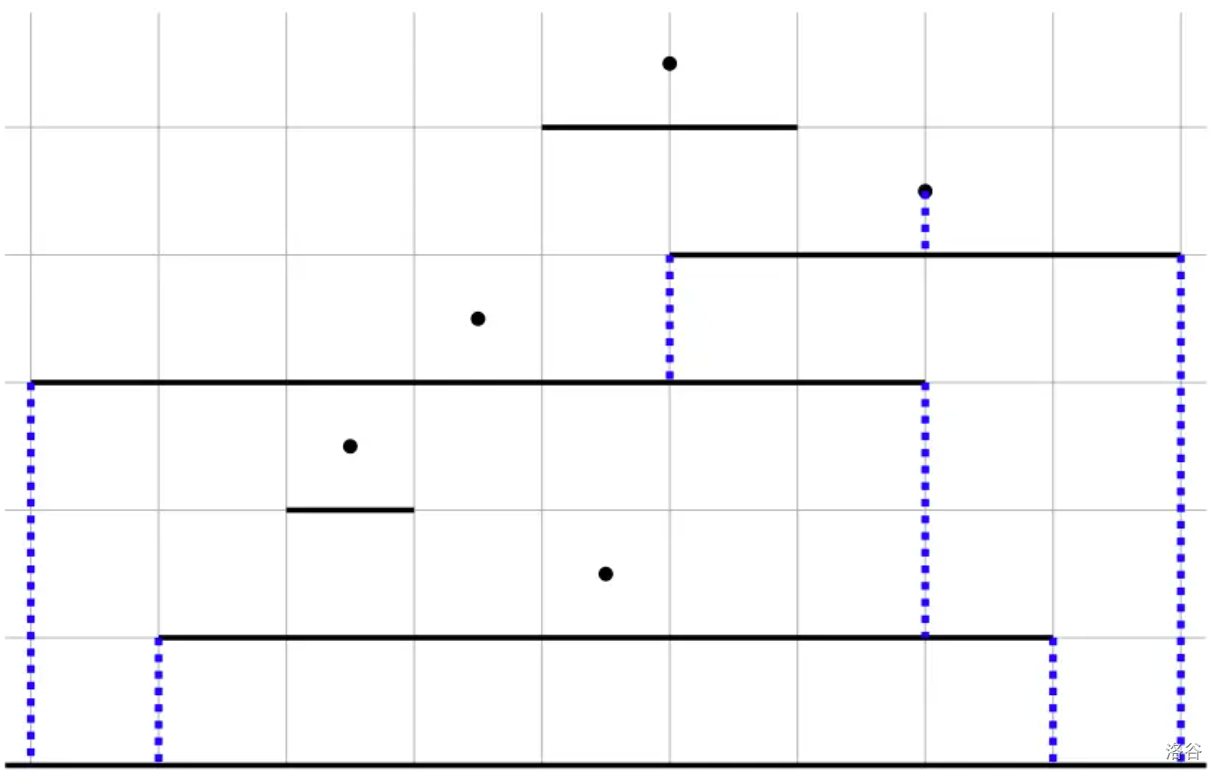  在第二组样例中，当打开一个水龙头时，水流的可视化效果. Radek 会按某个确定的顺序看水龙头的情况。当他看到第 $i$ 个水龙头时，当且仅当第 $i$ 个货架没被水淹，他才会打开这个水龙头。 Radek 还没确定他看水龙头的顺序。它会从 $n!$ 种顺序中均匀随机选择一种。Radek 想知道他平均会打开多少个水龙头。 你的任务是回答 Radek 的问题，给出答案对 $10^9+7$ 取模后的值。形式化地，令答案为 $\frac{p}{q}$，其中 $q\neq 0$ 且 $\gcd(p,q)=1$。你需要输出 $p\cdot q^{-1}\pmod{10^9+7}$，其中 $q^{-1}$ 是集合 $1,2,\ldots,10^9+6$ 中唯一满足 $q\cdot q^{-1}\equiv 1\pmod{10^9+7}$ 的整数。 可以证明对于所有满足题目条件的数据，结果是有理数，且分母不会被 $10^9+7$ 整除。

第一行一个整数 $n\ (1\le n\le 500\,000)$，表示 Mati 公司的货架数。 接下来 $n$ 行，第 $i$ 行有两个整数 $l_i,r_i\ (1\le l_i

输出一行一个整数，表示 Radek 平均需要打开多少水龙头。答案对 $10^9+7$ 取模后输出。

**样例解释 1** 让我们考虑在第一个样例中 Radek 看水龙头的所有顺序： - 按 $1,2,3$ 的顺序，他会打开所有 $3$ 个水龙头。 - 按 $1,3,2$ 的顺序，他会先打开水龙头 $1$ 和 $3$。当他准备打开水龙头 $2$ 时，水已经淹了第 $2$ 个货架，所以他不需要打开水龙头 $2$ 了。 - 按 $2,1,3$ 的顺序，他会打开所有 $3$​ 个水龙头。 - 按 $2,3,1$ 的顺序，他会先打开水龙头 $2$ 和 $3$。当他准备打开水龙头 $1$ 时，水已经淹了第 $1$ 个货架，所以他不需要打开水龙头 $1$ 了。 - 按 $3,1,2$ 或 $3,2,1$ 的顺序，由于打开水龙头 $3$ 后，所有货架都会被淹，因此就不需要再打开剩下的两个水龙头了。 Radek 平均需要打开 $\frac{1}{6}\cdot(3+2+3+2+1+1)=2$ 个水龙头。 **样例解释 2** 第二组样例中 Radek 平均要打开 $\frac{91}{30}$ 个水龙头，由于 $30^{-1}\equiv 233333335\pmod{10^9+7}$，所以输出 $91\cdot 233333335\equiv 21233333485\equiv 233333338\pmod{10^9+7}$。